属性加密：分段安全性

千呼万唤始出来！本文是我的 2019 年科研“属性加密”系列博文第五篇。之前一套“增加编程空间、递归模拟、树平衡化”组合拳，针对算术公式证明了 1-ABE 的适应性安全性，在这之后，我跌跌撞撞发现了最终记录在 [LL20] 里的一个关键性质：AKGS 分段安全性。这个性质大大简化了证明过程。

本篇首次打破了系列摘要开场白的队形，可见其重要程度。另外我发现上一篇里紧凑格式的文内导航似乎挺好，所以就沿用了。

文内导航 § 前情提要 § 平衡就一定好吗 § Mes Pensées Vagabondes § 具体例子 § 分段安全性 § 本篇结语 § 参考文献

前情提要

第一篇里介绍了属性加密 (ABE) 的概念，并定下了一个“小目标”——构造支持算术公式的 ABE。第二篇里定义了算术密钥乱码化方案 (arithmetic key garbling scheme) 即 AKGS，并构造了用于算术公式 (arithmetic formulae) 的 AKGS。

第三篇里介绍了 1-ABE 的概念（单个密钥、单个密文、随机消息下安全的私钥 ABE），用内积加密 (IPFE) 和 AKGS 构造了 1-ABE，并给出了一个诈和证明。第四篇讲述了历史上我想到的第一个正确证明。

平衡就一定好吗？

书承上回，对数深度算术公式的 1-ABE，适应性安全性可通过递归模拟来证明，因为算术公式可以平衡化到对数深度，要保证适应性安全证明对任意多项式规模的公式成功，只需要加入固定大小的编程空间。具体来说，深度为 $d$ 的算术公式证明时需要的编程空间 (programming space) 不超过 d，然而这个估计其实很多时候都很松。考虑公式 x1​x2​⋯x8​，它最平衡的版本是一颗满二叉树：

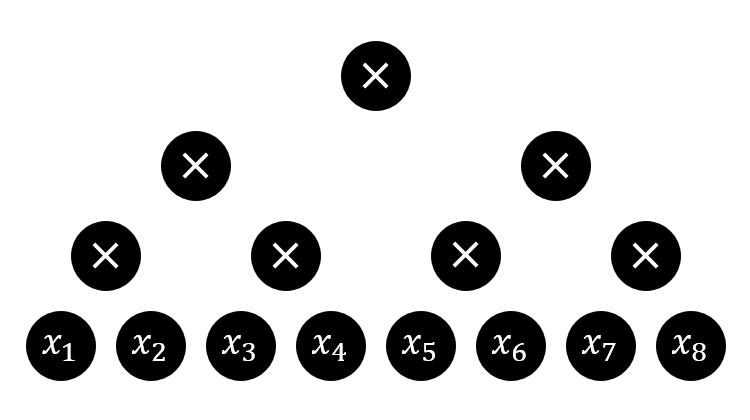
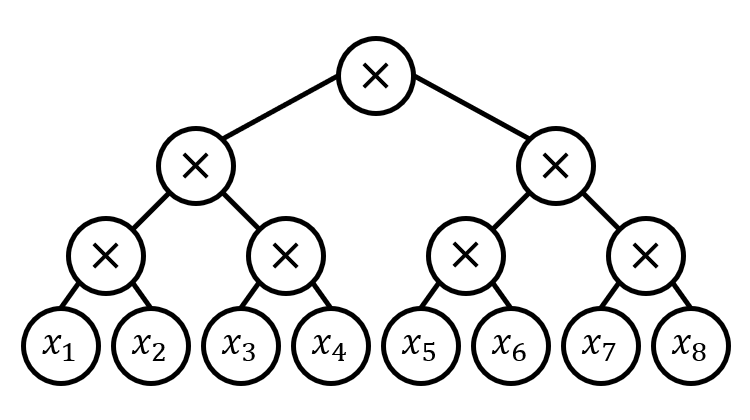
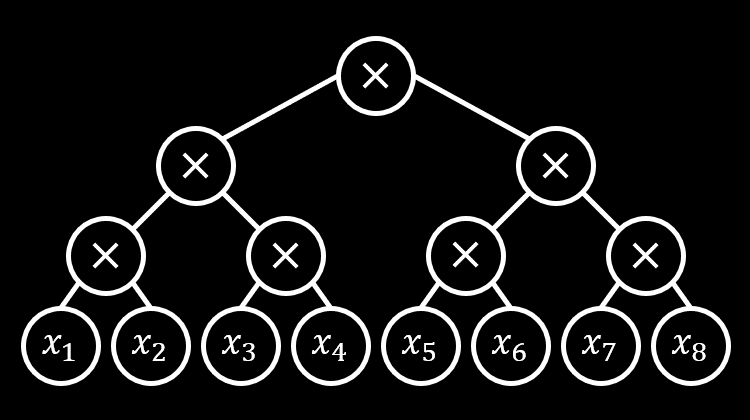
用这个公式树进行递归模拟，需要的编程空间是 4——$x_1,x_5,x_7,x_8$ 节点对应的标签某一时刻同时存在于 IPFE 密文中。如果考虑公式最不平衡的版本之一，左偏链：¹

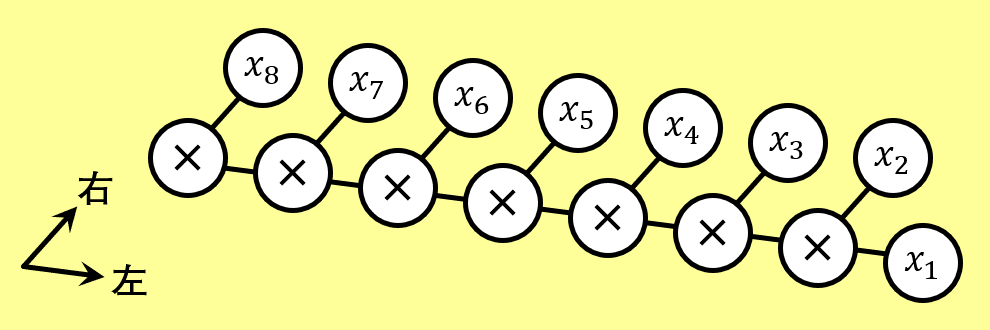
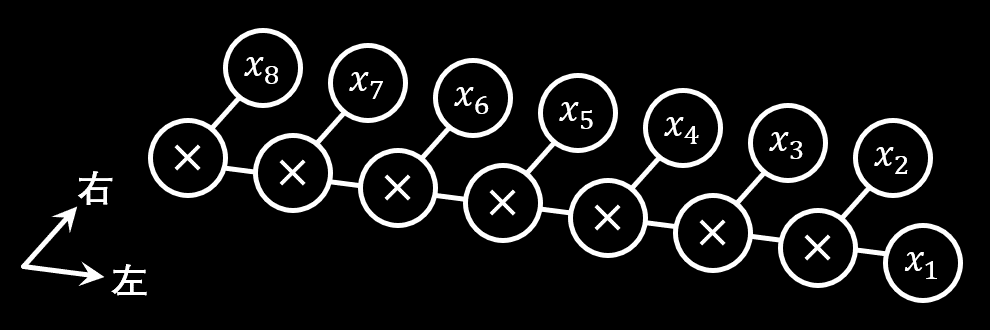
用这个公式树进行递归模拟，需要的编程空间是 2——同一时刻只有 $x_1,x_j$ 节点对应的标签存在于 IPFE 密文中，其中 $j$ 随着证明的进行从 2 变化到 8。

Mes Pensées Vagabondes

无脑对公式树平衡化只是为了让证明能走通，而不是真正优化证明所需要的编程空间。自然就要问：²

这个操作是必要之繁 (necessarius)，还是弥补我们证明技巧匮乏的补丁？

——沃·兹基硕德

回到 1-ABE 的证明，上面的例子是否表示使用不平衡树其实更好？但如果要求总是写成一条多项式长度的链，那么表达能力可能会大打折扣（不一定所有算术公式都能转换为多项式规模的链）。

如果我要求公式树的左子树深度总是大于右子树深度呢？这样做的理由是左子树递归结束后占用 1 个编程位置，此时右子树深度更小，或许需要的编程空间小于左子树途中用到的，这样总共使用的编程空间就不随着深度增加了……然而这个想象是错误的，只能得到 $$s(d)\le \max \{s(d-1),1+s(d-2)\},$$ 仍然只能证明 $s(d)=\mathcal{O}(d)$ 而不能得到更好的估计。

再换一个角度，连乘和连加（无论多少个变量）总是只需要 2 个额外位置，是否应该用³算术 AC（而不是算术 NC 电路）建模？捣鼓了一阵儿似乎也不是。

🤔当时我在想这个问题的时候觉得可以更具体感受一下这个证明过程，说不定会有什么新发现，于是就写了一套代码来表示算术公式树、输出乱码化结果、输出证明的每个中间步骤。有一天晚上（我觉得应该是 5 月 23 日），突然灵光一现💭💡，发现了神奇的结构，顿时想要冲出澡盆奔上大街大喊 Εύρηκα……咳咳，咱们还是先看一个具体例子。

具体例子

继续用我们一直用的例子，即 (2x1​−x2​)(x3​+3x2​)+(5x1​+1)x4​，在下图中令 α=μ,β=0。

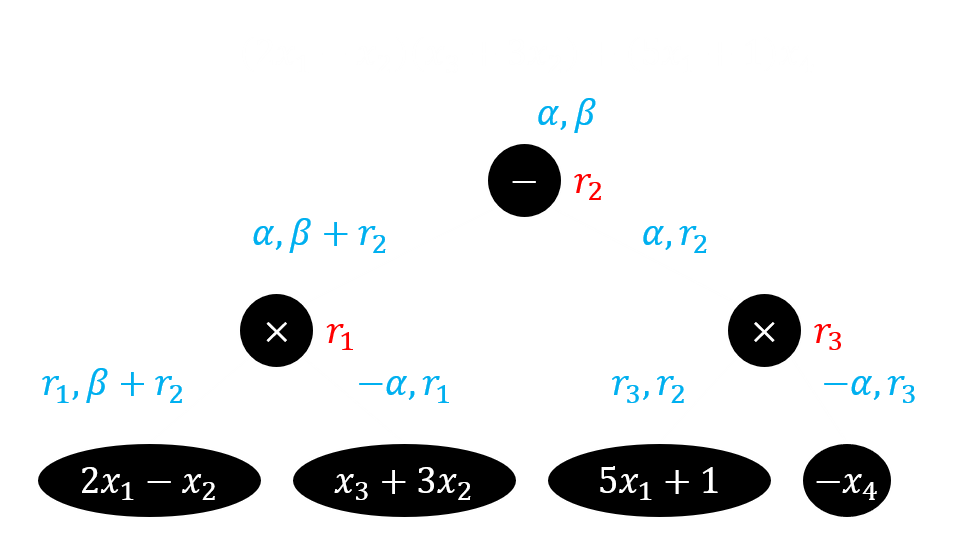
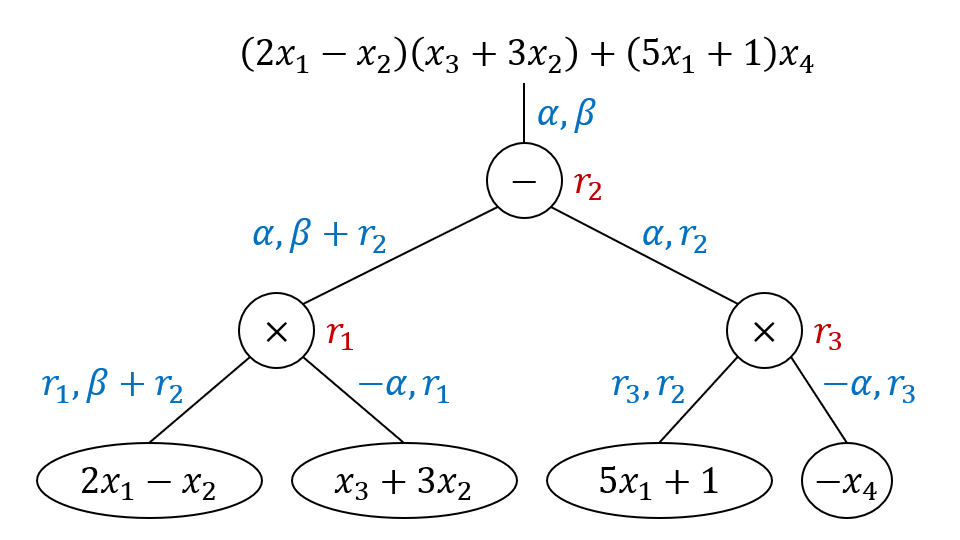
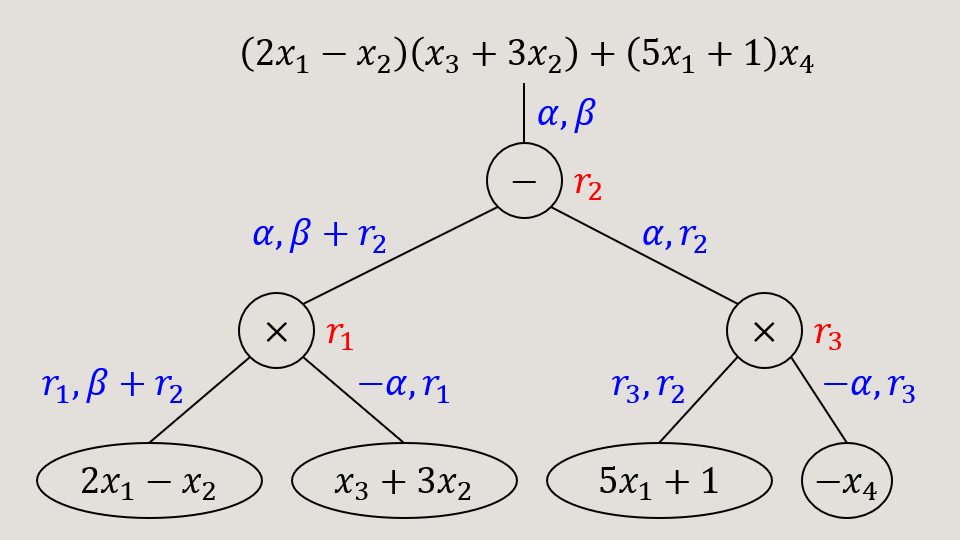
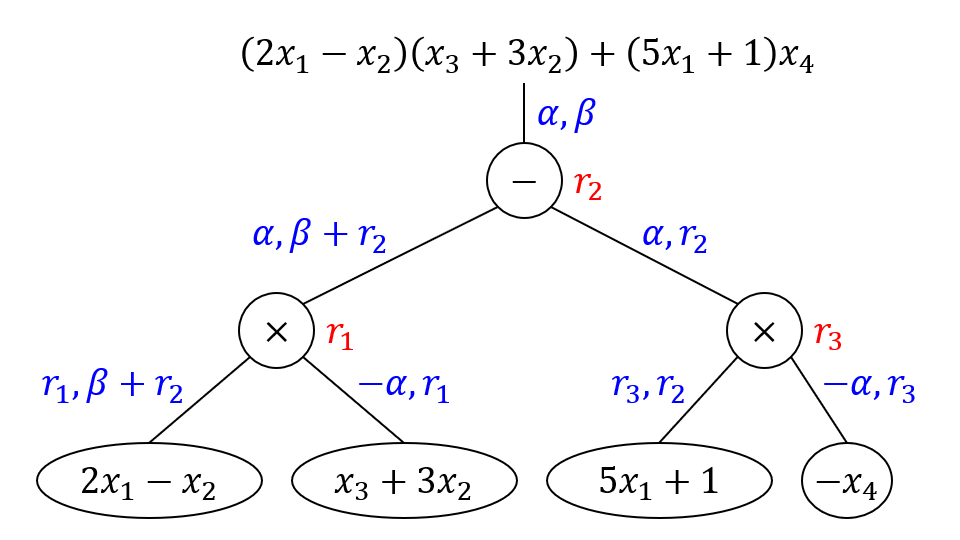
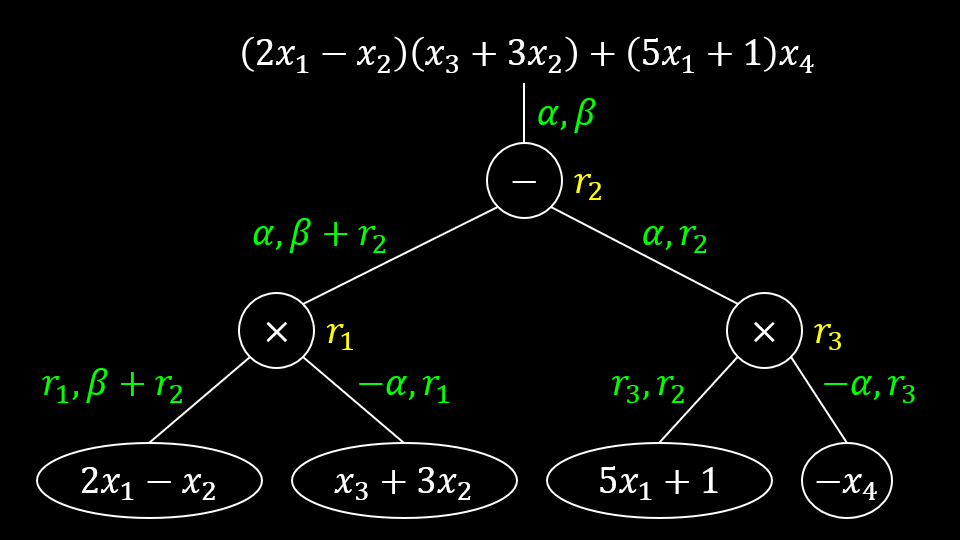
把标签写出来，是 $$\begin{array}{rl}{\ell }_1=L_1(\mathbf{x})& =2r_1{x}_1-r_1{x}_2+r_2,\\ {\ell }_2=L_2(\mathbf{x})& =-\mu x_3-3\mu x_2+\boxed{r_1},\\ {\ell }_3=L_3(\mathbf{x})& =5r_3{x}_1+r_3+\boxed{r_2},\\ {\ell }_4=L_4(\mathbf{x})& =\mu x_4+\boxed{r_3}.\end{array}$$ 和之前一样，我们要利用 $$\begin{array}{rl}{\ell }_1& =\mu ((2x_1-x_2)(x_3+3x_2)+(5x_1+1)x_4{)}^{=0}\\ & +{\ell }_2(2x_1-x_2)+{\ell }_3-{\ell }_4(5x_1+1)\\ & ={\ell }_2(2x_1-x_2)+{\ell }_3-{\ell }_4(5x_1+1).\end{array}$$ 但是这次我在上面的 ${\ell }_2,{\ell }_3,{\ell }_4$ 里分别框出了随机数 r1​,r2​,r3​。它们很特殊，$r_{j-1}$ 满足以下性质：

• 它在 ${\ell }_j$ 里以且仅以常数项出现。
• 对于 j′>j，它在 ${\ell }_{j^{\prime }}$ 里不出现。

$r_{j-1}$ 叫做 $L_j,{\ell }_j$ 的随机化子⁴ (randomizer)，先从标签的角度考虑如何从真实标签过渡到模拟标签，走如下几步：

1. 把 ${\ell }_1$ 从“用标签函数计算”改成“通过正确性和其他标签计算”。
2. 现在 $r_1\stackrel{{}_{\$}}{\leftarrow }{\mathbb{Z}}_p$ 只出现在 ${\ell }_2$ 中，且它以常数项出现，故可以把 ${\ell }_2$ 从“用标签函数计算”改成“设置为随机数”，分布不变。
3. 此时同理可把 ${\ell }_3$ 改成随机数。
4. 最后，再同理把 ${\ell }_4$ 改成随机数。

这个过程可以翻译成在 IPFE 里的证明：

1. 把 ${\ell }_1=L_1(\mathbf{x})$ 从 ${\mathsf{i}\mathsf{s}\mathsf{k}}_1$ 挪进 ict，再改用正确性约束计算 ℓ1​。
2. 对 $j=2,3,\dots$
   1. 把 ${\ell }_j=L_j(\mathbf{x})$ 从 ${\mathsf{i}\mathsf{s}\mathsf{k}}_j$ 挪进 ict。
   2. 现在我们已经消灭了所有下标 $<j$ 的标签函数（的系数），使用标签 ${\ell }_j$ 和所有下标 $>j$ 的标签函数，此时随机化子保证 ${\ell }_j$ 是独立均匀随机数，因此可以把它改成随机数。
   3. 现在 ${\ell }_j$ 和使坏者选择的 $\mathbf{x}$ 独立，所以可以挪回 ${\mathsf{i}\mathsf{s}\mathsf{k}}_j$ 里面。注意这一通操作也消灭了标签函数 Lj​。

动画演示 (≈ 1.8 MB) 白底黑字 | 黑底白字

动画演示 可在 https://geelaw.blog/entries/ll20a-piecewise-security/#animation 查看。

实际上，最开始我是把这个证明过程形容为 空当接龙 的（后来才用于形容泛函保密性的证明），可以认为第二个编程位置是空当接龙里的中转单元，而最终模拟时标签的位置时回收单元。

分段安全性

引理 先前构造的算术公式 AKGS 满足如下性质：

• $\mathsf{E}\mathsf{v}\mathsf{a}\mathsf{l}$ 里 ${\ell }_1$ 的系数恒不为零。
• 对任意 j>1：$r_{j-1}$ 在 $L_j$ 中仅出现在常数项中，且系数不为零；且对任意 j′>j，它不在 $L_{j^{\prime }}$ 中出现。

其中 $r_j$ 是树的中序 (in-order) 里第 $j$ 个非叶子节点上产生的随机数。

证明思路 考察递归过程中 $\alpha ,\beta$ 会怎样传播到叶子即可。细节留作读者习题。

上述性质最终命名为特殊分段安全性 (special piecewise security)，其中 special 用法类似于 special HVZK 中的用法。

如果只想要之前的证明策略（只用 2 个编程位置）成功，则可以考虑更一般的定义——分段安全性 (piecewise security)。简单来说，对 $\mathsf{E}\mathsf{v}\mathsf{a}\mathsf{l},{\ell }_1$ 的要求改成了可以通过其他标签和计算结果对 ${\ell }_1$ 逆向抽样，且这种抽样即使在给定 ${\mathbf{L}}_2,\dots ,{\mathbf{L}}_m$ 的条件分布下仍然完美；对标签函数随机化子的要求改成了每个 ${\ell }_{j>1}$ 在给定 ${\mathbf{L}}_{j+1},\dots ,{\mathbf{L}}_m$ 的条件分布是均匀随机。具体定义见 [LL20]。

引理 若某函数类具有分段安全的 AKGS，则可通过泛函保密的 IPFE 构造适用于该函数类对应的策略且适应性安全的 1-ABE。

本篇结语

这一篇讲了研究中的小故事，由算术公式 AKGS 递归模拟策略出发，从各种角度思考如何简化证明的过程，在思考过程中终于发现了有趣的新性质——分段安全性。

最近几篇深入了 1-ABE 构造和证明，暂时算是比较好地解决了 1-ABE 适应性安全的问题了，但别忘了咱们真正的目标是构造 ABE！下一篇理应开始思考如何把 1-ABE 转换为 ABE，不过我想稍微再谈谈分段安全性，所以会有一篇番外。敬请期待！

参考文献