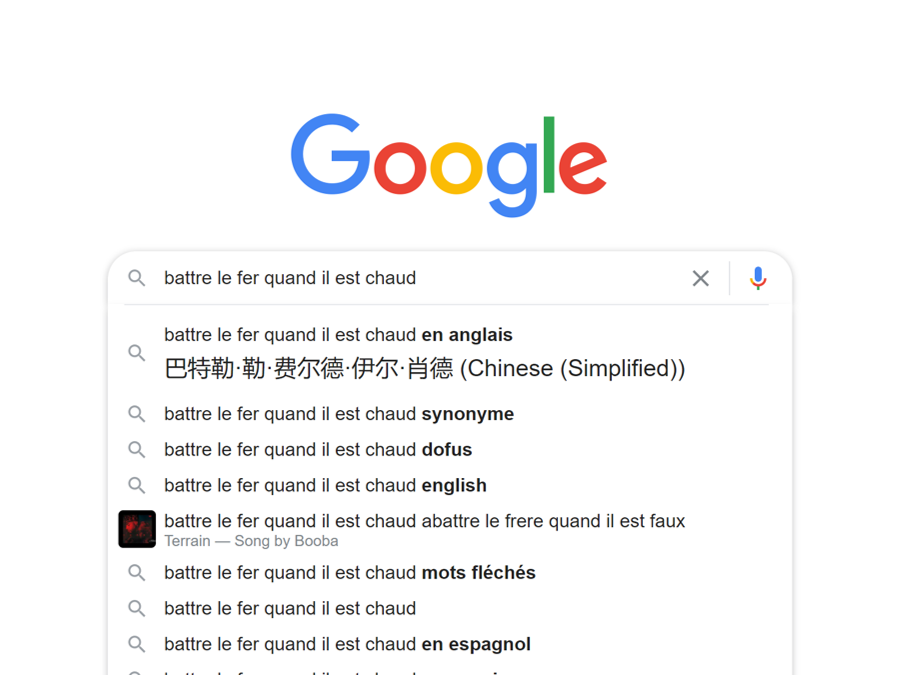
“趁热打铁”出自哪里？
“趁热打铁”是从法语翻译来的成语吗？
Gee Law’s Blog
新 Edge 标签页作为 Alt+Tab 切换项的评论
听闻最近 Windows 10 预览版里 Alt+Tab 可以切换（新）Edge 标签页，我有一些评论想要发表。另，最近忙了很多事儿，密码学研究系列久久未更，还在计划重写博客网站，烦呀！
一点微小的 OneNote 使用经验
我最近写的一个知乎答案，简单说说我使用 OneNote 管理研究笔记一点微小的经验。🐸
CRTP in C♯: static polymorphism and friendship
Another therapy session for my Performance-Obsessive Disorder.
蜜汁翻译
本篇收录作者在拒绝欧式汉语硬译甚至不译一些词汇时遇到的一些搞笑又（自认为）贴切的谜之翻译。
Performance-obsessive disorder, or generics and duck typing in C♯
POD (Performance-Obsessive Disorder) is an intended pun for Plain Old Data. This entry imagines how IEnumerable<T> of .NET could be upgraded for better performance, featuring duck typing with generics.
Blogging my blog
A meta-blog that keeps the trace of my blog site. The latest update reinforces the design goal of the website.
属性加密（番外）：分段安全性的故事
这一篇是我的 2019 年科研“属性加密”系列番外篇，记录一些关于（特殊）分段安全性的故事。这一篇的风格相较主系列更轻松活泼（肯定有人要吐槽我对“轻松活泼”的定义），比如去掉了繁复的导航按钮，减少了公式。另外这一篇也加上了“数学”的标签，大概是因为很多这里考虑的问题的密码学价值不大，更像是线性代数的游戏？
属性加密：分段安全性
千呼万唤始出来！本文是我的 2019 年科研“属性加密”系列博文第五篇。之前一套“增加编程空间、递归模拟、树平衡化”组合拳，针对算术公式证明了 1-ABE 的适应性安全性，在这之后，我跌跌撞撞发现了最终记录在 [LL20] 里的一个关键性质：AKGS 分段安全性。这个性质大大简化了证明过程。
