Notes for UMich EECS 598 (2015): Lecture 2

Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for lecture 2, SVP, Gram–Schmidt, LLL.

In this note, I write down a cheatsheet as well as my questions. Due to the nature of personal notes, I will not formally put references.

Definition 1.1/1.2. SVP = Shortest (non-zero) Vector Problem. Given a lattice basis, find information about the shortest non-zero vector in the lattice.

Decision is to tell whether the shortest non-zero vector has length greater than / not greater than given bounds. The important problem is $G a p S V P_{γ},$ to tell whether the length is $\leq d$ or $> γ d .$
Calculation / estimation is to compute / approximate the length of the shortest non-zero vector. The important problem is $E s t S V P_{γ},$ to output $d \in [λ_{1}, γ λ_{1}] .$
Calculation / estimation is to compute / approximate the length of the shortest non-zero vector. The important problem is $S V P_{γ},$ to output a non-zero lattice point $v$ s.t. $∣ v ∣ \leq γ λ_{1} .$

Question. Why doesn’t $E s t S V P_{γ}$ consider two-sided approximation? What if we allow the algorithm to output anything in $[\frac{λ _{1}}{γ}, γ λ_{1}] ?$

Clearly, for $γ \geq 1,$ it holds that $G a p S V P_{γ} \leq E s t S V P_{γ} \leq S V P_{γ} .$ Moreover, we know (and will prove later) that $S V P_{1} \leq G a p S V P_{1} \dots$

Note that the reduction using binary search needs to make sure the initial range is bounded by $2^{poly},$ and the lecture note does so by using Minkowski’s bound. This is an overkill, because the minimum distance is at most $∣ b_{1} ∣,$ which is bounded by $2^{poly} .$

Open Problem 1.3. … However, it is unknown for any polynomial $γ$ strictly greater than 1 whether $S V P_{γ} \leq G a p S V P_{γ} .$

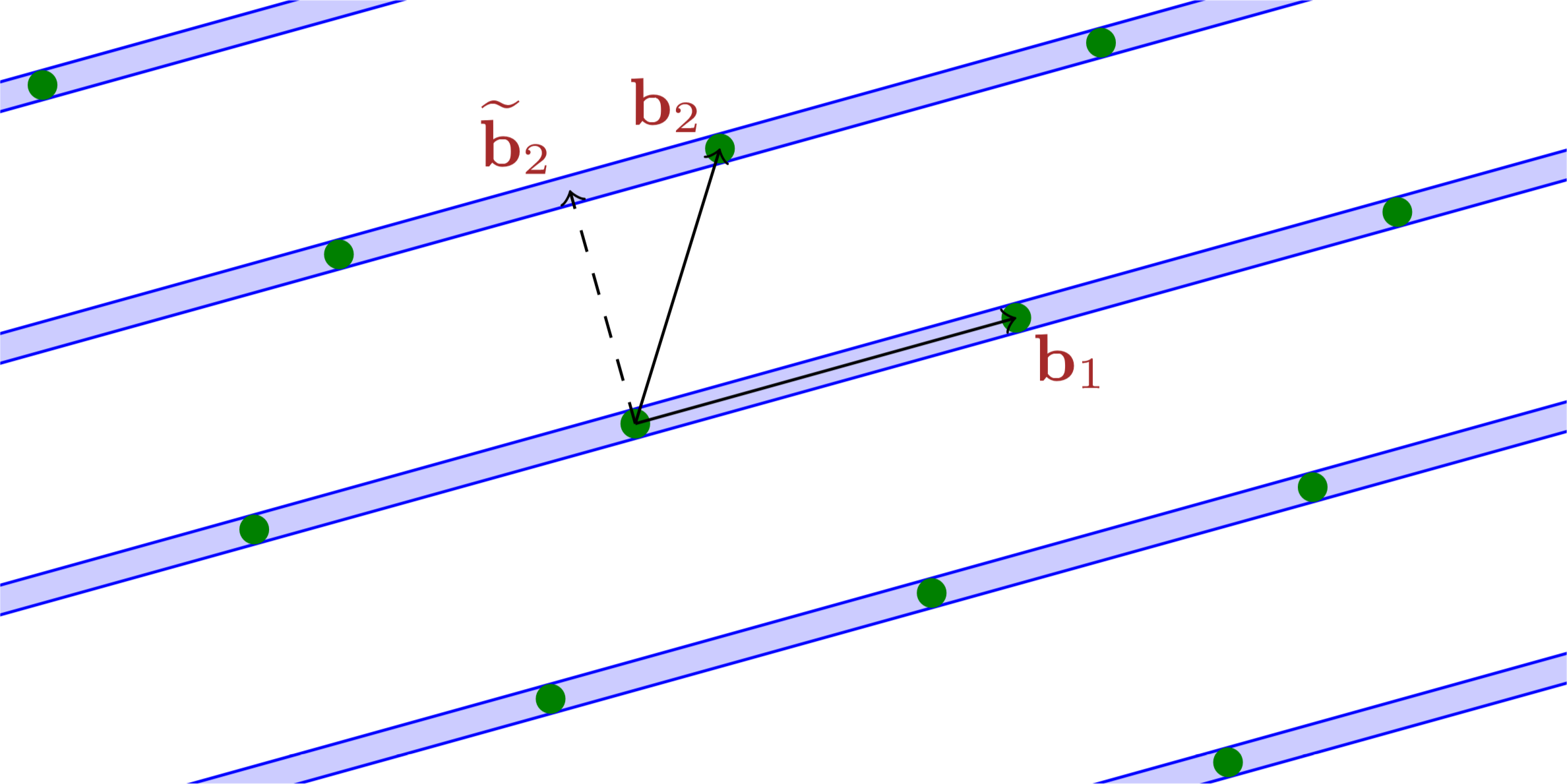
Example of Gram–Schmidt orthonormalisation (by Chris Peikert)

Lemma 2.3. The proof in the lecture note suggests that taking advantage of upper-unitriangularity of $U$ could be a useful technique to deal with Gram–Schmidt vectors of a lattice basis. Both upper-triangularity and the fact that the diagonals are one are important.