Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for lecture 2, SVP, Gram–Schmidt, LLL.
In this note, I write down a cheatsheet as well as my questions. Due to the nature of personal notes, I will not formally put references.
Definition 1.1/1.2. SVP = Shortest (non-zero) Vector Problem. Given a lattice basis, find information about the shortest non-zero vector in the lattice.
- Decision is to tell whether the shortest non-zero vector has length greater than / not greater than given bounds. The important problem is to tell whether the length is or
- Calculation / estimation is to compute / approximate the length of the shortest non-zero vector. The important problem is to output
- Calculation / estimation is to compute / approximate the length of the shortest non-zero vector. The important problem is to output a non-zero lattice point s.t.
Question. Why doesn’t consider two-sided approximation? What if we allow the algorithm to output anything in
Clearly, for it holds that Moreover, we know (and will prove later) that
Note that the reduction using binary search needs to make sure the initial range is bounded by and the lecture note does so by using Minkowski’s bound. This is an overkill, because the minimum distance is at most which is bounded by
Open Problem 1.3. … However, it is unknown for any polynomial strictly greater than 1 whether
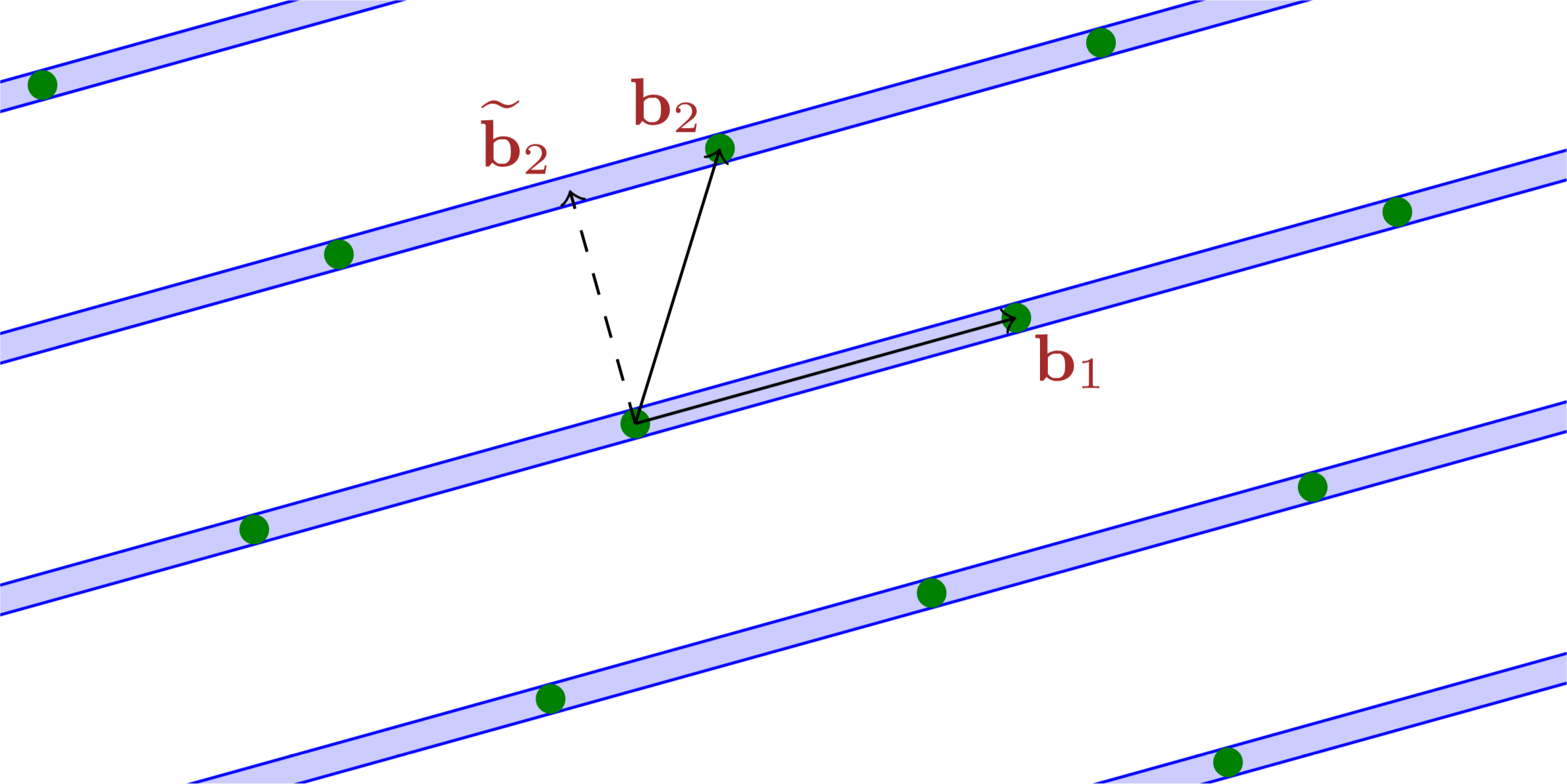
Lemma 2.3. The proof in the lecture note suggests that taking advantage of upper-unitriangularity of could be a useful technique to deal with Gram–Schmidt vectors of a lattice basis. Both upper-triangularity and the fact that the diagonals are one are important.
Please enable JavaScript to view the comments powered by Disqus.