属性加密：修复诈和

本文是我的 2019 年科研“属性加密”系列博文第四篇。这次揭晓上回的小悬念：解释上次的证明怎么错了，然后讨论针对算术公式的一个自然的修复思路。这个思路最终启发我发掘出了 LL20 中的一个关键概念，但这段故事本身并未记载在文献中，因此这一篇也肩负着重要使命：讲述文献“冰冷的美丽”背后“火热的思考”。

先插段题外话，“冰冷的美丽”“火热的思考”语出 Freudenthal Fre02：

No mathematical idea has ever been published in the way it was discovered. Techniques have been developed and are used, if a problem has been solved, to turn the solution procedure upside down, or if it is a larger complex of statements and theories, to turn definitions into propositions, and propositions into definitions, the hot invention into icy beauty.

不知为何，人们常把这句归于 Freudenthal 做编辑的一本 1960 年的会议纪要 (conference proceeding) Fre61。例如 Wikiquote 说这一句出现在会议纪要的第 9 页（罗马数字编号），但 Springer 的存档显示罗马数字编号的只有 6 页。目前我在 1961 年这本纪要里没有找到这句话，就只有 2002 年的书里找到了。

就我们的工作 LL20 来说，论文版本引入新发现的方式仍然很自然，不至于让人有“这也能行”的感觉，不过它的叙述和历史发展出入较大。记住事情发展过程算是我个人的浪漫，这就让博客来完成吧！

文内导航前情提要诈和揭秘递归模拟算术公式具体例子思路整理本篇结语参考文献

显示英汉术语对照

前情提要

第一篇里介绍了属性加密 (ABE) 的概念，并定下了一个“小目标”——构造支持算术公式的 ABE。第二篇里定义了算术密钥乱码化方案 (arithmetic key garbling scheme) 即 AKGS，并构造了用于算术公式 (arithmetic formulae) 的 AKGS。

第三篇里介绍了 1-ABE 的概念（单个密钥、单个密文、随机消息下安全的私钥 ABE），用内积加密 (IPFE) 和 AKGS 构造了 1-ABE，并给出了一个看似 OK 的证明。不过那个证明有 bug。这一篇解释之前的证明错在哪儿，并给出第一个修复思路。

诈和揭秘

回忆上次的证明，过渡博弈 $H_{1}$ 里，所有 IPFE 密钥 $i s k_{j}$ 里的标签函数 (label functions) 都抹掉了，而标签 (labels) $ℓ_{j} = L_{j} (x)$ 写死 (hardwire) 在和 1 相乘的位置。这是证明里首次出错之处。因为博弈是适应性的，使坏者 (adversary) 完全可以选择先请求算术公式 $f$ 的密钥，再请求属性 $x$ 的密文，如此一来，在回答密钥请求时就不知道 $x$ 是什么，也就不知道 $ℓ_{j} = L_{j} (x)$ 是多少，即不知道该把什么写死在 IPFE 密钥里。

一个非常朴素 (naïve)¹的想法是说，使坏者能做的基本上也就是尝试一下 AKGS 求值算法，所以可以直接这样证明：在过渡博弈里直接把 IPFE 密钥里的标签函数改成由一个完全不相干的 $\overset{μ}{˙}$ 乱码化而来的，因为 IPFE 密文、密钥内积的分布保持不变，由 IPFE 安全性保证过渡博弈和真实博弈不可区分。

事与愿违，IPFE 安全性只保证内积本身不变时的不可区分性，因此上述论证无法形式化成功。此外，从归约的角度考虑，归约算法需要向 IPFE 安全定义的挑战者 (challenger) 提交两组向量，如果向量内积不同，那么归约算法本身是可以轻松区分两者的。不过这不代表使坏者就可以区分，一个可能的场景是归约算法有使坏者无法访问的私有随机数（譬如 AKGS 乱码化算法所用的随机数），这导致使坏者仍然无法区分两者。但无论如何，之前那种朴素的证明思路似乎很难²转换为形式化证明。

继续思考之前诈和证明的思路，可以发现它有一个更致命的问题。即最终过渡博弈 $H_{2}$ 也天然需要提前知道 $x$ 才能进行，因为模拟算法 $S i m$ 需要知道 $x$ 才能调用。读者自然会问： $S i m$ 真的需要知道 $x$ 吗，还是这只是定义上的疏忽，其实不需要？很可惜，答案是“真的需要”，至少模拟出的标签应当满足 $E v a l$ 正确性约束，否则可以轻松和真实标签相区分。这表示“容易想象”的正确证明绝不可能到达之前诈和证明里的 $H_{2}$ 过渡博弈。

妥协方案 1 是只考虑选择性安全 (selective security)，即使坏者必须一开始就决定挑战属性 $x 。$ 毕竟真实世界不关心³适应性安全性。一方面，目前的方案看起来没有明显破绽，很容易信仰⁴“虽然没能证明适应性安全，但其实是安全的”；另一方面，可以轻松⁵分离 (separate) 适应性安全和选择性安全，安全性当然是高高益善。

妥协方案 2 是使用作弊手段——撬动复杂性杠杆 (complexity leveraging) ——获得适应性安全性。具体来说，首先证明选择安全性，然后通过“猜出 $x ”$ 的方法把适应性安全归约为选择性安全。这个方法的问题在于它会产生指数级别的安全性损失，因此一开始的方案必须具有指数级安全性才行。后面我们会再提到这件事。

i s k_{1} i s k_{2} ⋮ i s k_{m} i c t 1000 ℓ_{1} 0100 ℓ_{2} \dots \dots ⋱ \dots \dots 0001 ℓ_{m}

妥协方案 3 证明思路里的过渡博弈

妥协方案 3 是在使坏者“先 $f$ 后 $x ”$ 时把所有标签都写死到 IPFE 密文不同位置上，而 IPFE 密钥里只在对应位置上放 1，这一步用到 IPFE 泛函保密性 (function-hiding)，然后再用 AKGS 模拟安全性即可。这样做需要升高 IPFE 的维度来提供编程空间 (programming space)，如图所示。这带来的后果就是 $f$ 的乱码化规模不能任意大，或者说只有当 $f$ 乱码化规模足够小时才能证明安全性，对于算术公式来说，这要求公式本身的规模足够小。

当初定“小目标”时我提醒过，支持任意规模的算术公式会是难点之一。当时研究就卡在这里不动了，于是我读了 KW19，它证明只要猜出关于 $x$ 的部分信息即可完成。这是一种精妙版本的妥协方案 2，然而再度思考表明这个方法对算术公式似乎不太好使。这是因为 DDH 假设在阶为 $p$ 的循环群里的区分优势可以平凡达到 $Ω (1 / p^{2}) ，$ 仅仅猜 $x$ 的两个坐标（产生 $p^{2}$ 的安全损失）对安全性也是致命打击。

虽然我没有想出什么特别好的方法，不过我导师有更“透过现象”的眼光，她表示这个证明过程可以高度概括为“小状态模拟”，所以提示我也可以尝试一下类似的东西。Bingo! 第一个解决方案就此诞生。另外，虽然这方法是读了 KW19 之后受启发而想到的，但实际操作起来截然不同。

↩¹ “朴素”是 naïve 一词比较专业的翻译，调皮起来的话也可以说是“幼稚”，但有朴素的想法不是什么坏事儿。

↩² 形式化刻画什么叫“适应性选择的、内积分布相同的两组向量”就已经够困难的了。

↩³ 或许更准确来说是现实世界的人不关心适应性安全的证明。对理论爱好者来说，可证明安全举足轻重，关于可证明安全的讨论可参考 Bel98 KM07 Dam07，特别推荐 Ivan Damgård 那篇议论文里 non-committing encryption 的例子。此外，我相信当前方案只需要一点点 $q -$ 型假设 $(q -$ type assumption) 即可证明适应性安全性，但追求更简单干净的假设依然是重要课题。

↩⁴ 这种想法实际上非常危险：安全性是高度非平凡的性质，如果没有专门去实现，它通常不会存在；此外，一个人现在想不到攻击策略，不代表其他人以后想不到攻击策略。

↩⁵ 具体来说，“分离”是指如下命题：假设存在着适应性安全的 ABE，则可以构造一个新 ABE，它满足选择安全性，且可以显式构造适应性攻击。证明留作读者习题，提示：向适应性安全的 ABE 中加入一个随机弱点，且弱点随 ABE 密钥透露。注意，构造出来的方案显然不符合任何现实世界里构造安全加密算法的工程准则，但仍然符合形式化定义的安全性，这种叫做刻意反例（即 contrived counter-example）。它警醒人们：形式化定义不总是和直觉相称。这当然不是说形式化定义安全性没有意义，作为密码学研究者，应该尽量发掘好的定义，既要精确又要能够恰当刻画直觉。

递归模拟算术公式

之前的证明思路是一般化使用 AKGS 模拟算法，而我们的“小目标”只针对算术公式，自然想到利用算术公式模拟算法的特殊结构。之前提到过模拟算法产生的标签必须满足 $E v a l$ 正确性，对于算术公式来说，这实际上是标签分布的惟一约束。用归纳法容易证明：

命题对于展开成树的算术公式 $f ，$ 它的模拟算法等效于设置除了最左叶子节点对应的标签 $ℓ_{2}, \dots, ℓ_{m}$ 为若干独立随机数，再求解满足 $E v a l$ 正确性的对应于最左叶子的标签 $ℓ_{1} 。$ 且 $E v a l (f, x, ℓ_{1}, \dots, ℓ_{m}) = γ$ 是关于 $ℓ_{1}$ 的一次方程，且 $ℓ_{1}$ 系数等于 1。

注意模拟算法里除了 $ℓ_{1}$ 都和 $x$ 无关，结合妥协方案 3 里把标签放在 IPFE 密文里的思路，可以想象用如下的过渡博弈作为模拟：

$i s k_{2}, \dots, i s k_{m}$ 分别存储随机抽样的 $ℓ_{2}, \dots, ℓ_{m} ，$ 它们和 $i c t$ 里的 1 相乘。
$i c t$ 额外存储通过正确性约束算出的 $ℓ_{1} ，$ 而 $i s k_{1}$ 里放一个 1，它们俩相乘。

这里只考虑了比较困难的“先 $f$ 后 $x ”$ 的情况，注意这次至少模拟博弈良定义——任何时刻需要回答的内容，都知道怎么回答。那么下一个问题自然是要问：模拟博弈和真实博弈不可区分吗？怎么证明？

IPFE 安全性只允许我们切换内积相等的向量，仅仅分布相同是不行的，所以至少没法一步证明不可区分性。这时就要请我们最爱的过渡证明法 (hybrid argument) 出场啦！算术公式乱码化、求值、模拟、上述命题证明全都依据算术公式树的结构递归进行，自然想到要递归过渡到模拟博弈，为此我们需要推广一下刚刚的命题：

推广之前说的模拟也可“局部化”，即可以把算术公式树若干无祖先后代关系的节点设置为“模拟根”，它们的叶子通过随机 + 相对于这些“模拟根”的局部正确性约束模拟（其他叶子正常计算），其中“模拟根”的 $α, β$ 是从根节点根据乱码化算法递归算出的。

我觉得先看一个具体例子比较好理解，我特意把这个例子写得非常接地气、非常详细，希望能帮助读者感受过渡过程。

具体例子

沿用之前的例子，即 $(2 x_{1} - x_{2}) (x_{3} + 3 x_{2}) + (5 x_{1} + 1) x_{4} ，$ 它的乱码化过程如下图，注意在 1-ABE 中 $α = μ, β = 0 。$

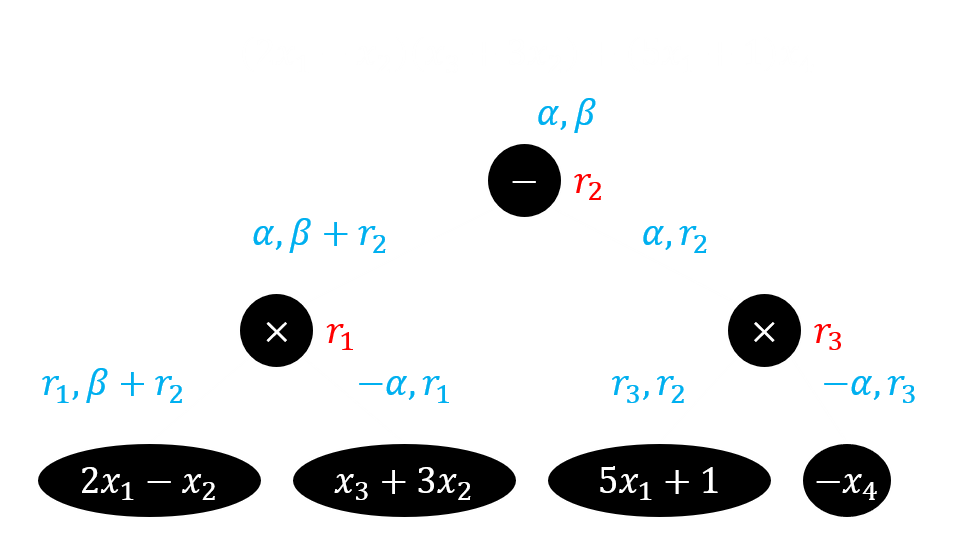
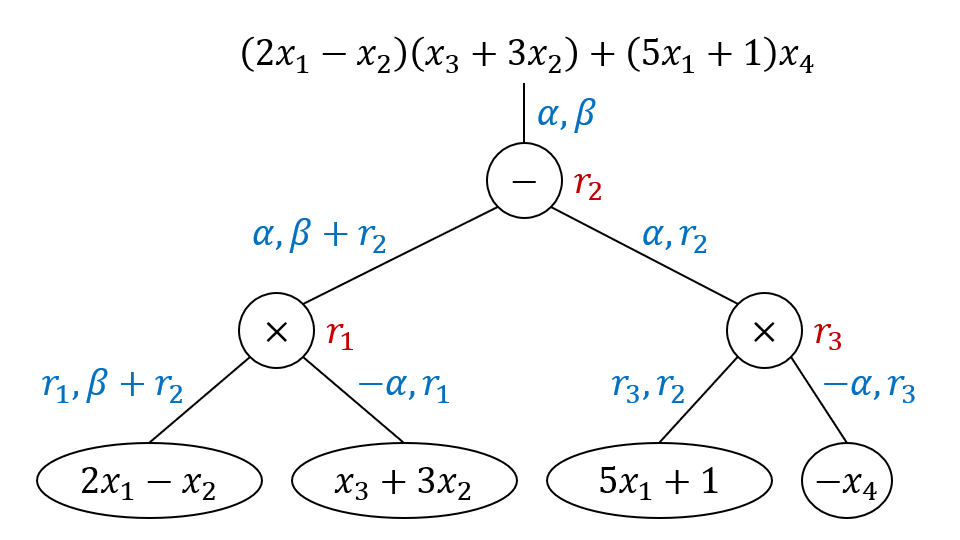
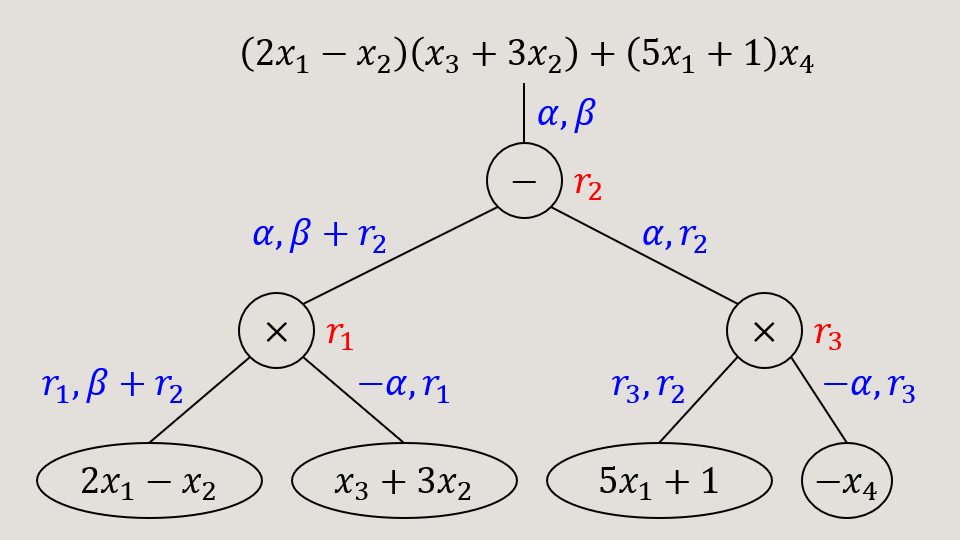
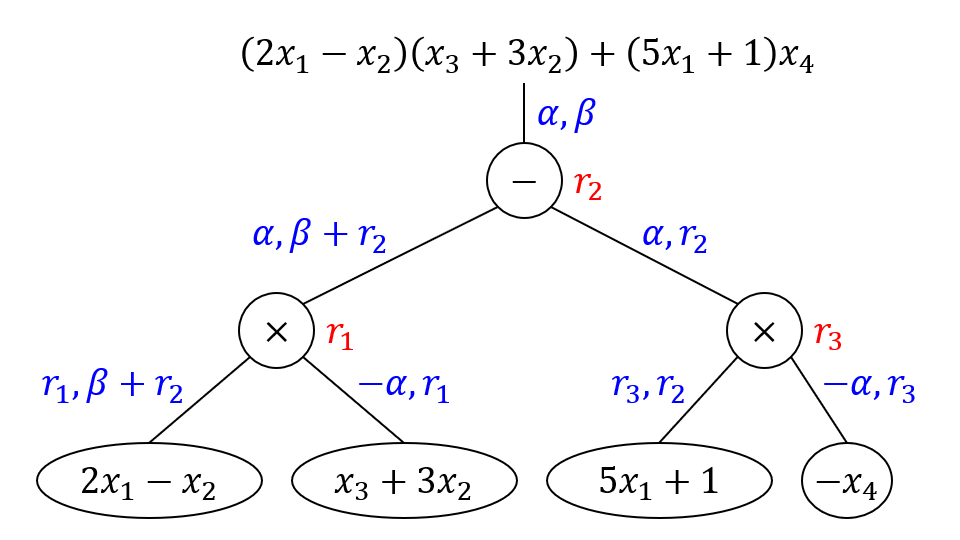
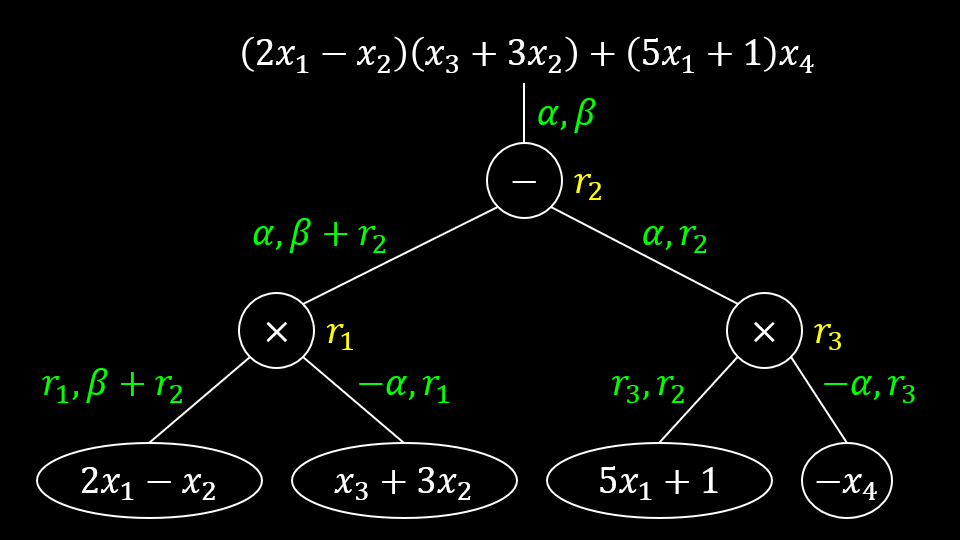
模拟需要 10 步过渡才能完成，并且要借助 3 个额外维度作为编程空间。图示含义如下：（也对读屏器可见）

实线节点是叶子节点。蓝色表示叶子对应的标签正常计算，红色表示由（局部）正确性模拟出的标签，绿色表示随机标签。节点内的文字和是否实心表示标签或标签函数是位于 IPFE 密文还是密钥中。
虚线节点是非叶子节点。黑白无特殊含义，黄色表示模拟依赖该节点的局部正确性，该节点的最左叶子必然是红色，它的其他叶子必然是绿色。
高亮单元格表示向量设置方法和上一个过渡博弈不同。
带框公式表示标签的计算方式和上一个过度博弈不同。

提示访问 https://geelaw.blog/entries/ll20a-initial-fix/ 以交互式查看例子。

提示您已禁用 JavaScript，启用后可交互式查看这个例子。

这个例子是交互式程序，通过按钮浏览博弈是如何过渡的吧！

Exp 1-ABE

sksksksk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	L1	0	0	0
$i s k_{2}$	L2	0	0	0
$i s k_{3}$	L3	0	0	0
$i s k_{4}$	L4	0	0	0
$i c t$	$1, x$	0	0	0

标签计算方式和其他说明。

$E x p_{1-ABE}$

sksksksk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$L_{1}$	$0$	$0$	$0$
$i s k_{2}$	$L_{2}$	$0$	$0$	$0$
$i s k_{3}$	$L_{3}$	$0$	$0$	$0$
$i s k_{4}$	$L_{4}$	$0$	$0$	$0$
$i c t$	$1, x$	$0$	$0$	$0$

标签计算方式为 $ℓ_{1} ℓ_{2} ℓ_{3} ℓ_{4} = L_{1} (x) = 2 r_{1} x_{1} - r_{1} x_{2} + r_{2}, = L_{2} (x) = - μ x_{3} - 3 μ x_{2} + r_{1}, = L_{3} (x) = 5 r_{3} x_{1} + r_{3} + r_{2}, = L_{4} (x) = μ x_{4} + r_{3} .$

$H_{1}$

ctsksksk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$L_{2}$	$0$	$0$	$0$
$i s k_{3}$	$L_{3}$	$0$	$0$	$0$
$i s k_{4}$	$L_{4}$	$0$	$0$	$0$
$i c t$	$1, x$	$ℓ_{1}$	$0$	$0$

$H_{2}$

ctctsksk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$0, 0$	$0$	$1$	$0$
$i s k_{3}$	$L_{3}$	$0$	$0$	$0$
$i s k_{4}$	$L_{4}$	$0$	$0$	$0$
$i c t$	$1, x$	$ℓ_{1}$	$ℓ_{2}$	$0$

$H_{3}$

ctctsksk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$0, 0$	$0$	$1$	$0$
$i s k_{3}$	$L_{3}$	$0$	$0$	$0$
$i s k_{4}$	$L_{4}$	$0$	$0$	$0$
$i c t$	$1, x$	$ℓ_{1}$	$ℓ_{2}$	$0$

标签计算方式为 $ℓ_{1} ℓ_{2} ℓ_{3} ℓ_{4} = μ (2 x_{1} - x_{2}) (x_{3} + 3 x_{2}) + r_{2} + ℓ_{2} (2 x_{1} - x_{2}), \leftarrow_{$} Z_{p}, = L_{3} (x) = 5 r_{3} x_{1} + r_{3} + r_{2}, = L_{4} (x) = μ x_{4} + r_{3} .$ 这相当于在上一个过渡博弈里作换元 $r_{1} = = def γ_{1} + μ x_{3} + 3 μ x_{2} ，$ 则 $γ_{1} \leftarrow_{$} Z_{p} ，$ 用 $γ_{1}$ 表示其他式子里的 $r_{1} ，$ 再把 $γ_{1}$ 重命名为 $ℓ_{2}$ 即得上式。另一种导出 $ℓ_{1}$ 的公式的方法是考虑它亲代节点上的局部正确性，即要求 $ℓ_{1}, ℓ_{2}$ 进行求值后可以正确算出它们亲代节点在整个求值过程的中间值，这等于是说 $ℓ_{1}$ 是惟一满足 $ℓ_{1} - ℓ_{2} (2 x_{1} - x_{2}) = μ (2 x_{1} - x_{2}) (x_{3} + 2 x_{2}) + r_{2}$ 的数。

$H_{4}$

ctsksksk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$ℓ_{2}, 0$	$0$	$0$	$0$
$i s k_{3}$	$L_{3}$	$0$	$0$	$0$
$i s k_{4}$	$L_{4}$	$0$	$0$	$0$
$i c t$	$1, x$	$ℓ_{1}$	$0$	$0$

$H_{5}$

ctskctsk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$ℓ_{2}, 0$	$0$	$0$	$0$
$i s k_{3}$	$0, 0$	$0$	$1$	$0$
$i s k_{4}$	$L_{4}$	$0$	$0$	$0$
$i c t$	$1, x$	$ℓ_{1}$	$ℓ_{3}$	$0$

$H_{6}$

ctskctct

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$ℓ_{2}, 0$	$0$	$0$	$0$
$i s k_{3}$	$0, 0$	$0$	$1$	$0$
$i s k_{4}$	$0, 0$	$0$	$0$	$1$
$i c t$	$1, x$	$ℓ_{1}$	$ℓ_{3}$	$ℓ_{4}$

$H_{7}$

ctskctct

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$ℓ_{2}, 0$	$0$	$0$	$0$
$i s k_{3}$	$0, 0$	$0$	$1$	$0$
$i s k_{4}$	$0, 0$	$0$	$0$	$1$
$i c t$	$1, x$	$ℓ_{1}$	$ℓ_{3}$	$ℓ_{4}$

标签计算方式为 $ℓ_{1} ℓ_{2} ℓ_{3} ℓ_{4} = μ (2 x_{1} - x_{2}) (x_{3} + 3 x_{2}) + r_{2} + ℓ_{2} (2 x_{1} - x_{2}), \leftarrow_{$} Z_{p}, = - μ (5 x_{1} + 1) x_{4} + r_{2} + ℓ_{4} (5 x_{1} + 1), \leftarrow_{$} Z_{p} .$ 这相当于在上一个过渡博弈里作换元 $r_{3} = = def ℓ_{4} - μ x_{4} 。$ 从局部正确性的角度看， $ℓ_{3}$ 是如下方程的惟一解： $ℓ_{3} - ℓ_{4} (5 x_{1} + 1) = - μ (5 x_{1} + 1) x_{4} + r_{2} .$

$H_{8}$

ctskctsk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$ℓ_{2}, 0$	$0$	$0$	$0$
$i s k_{3}$	$0, 0$	$0$	$1$	$0$
$i s k_{4}$	$ℓ_{4}, 0$	$0$	$0$	$0$
$i c t$	$1, x$	$ℓ_{1}$	$ℓ_{3}$	$0$

$H_{9}$

ctskctsk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$ℓ_{2}, 0$	$0$	$0$	$0$
$i s k_{3}$	$0, 0$	$0$	$1$	$0$
$i s k_{4}$	$ℓ_{4}, 0$	$0$	$0$	$0$
$i c t$	$1, x$	$ℓ_{1}$	$ℓ_{3}$	$0$

标签计算方式为 $ℓ_{1} ℓ_{2} = μ ((2 x_{1} - x_{2}) (x_{3} + 3 x_{2}) + (5 x_{1} + 1) x_{4}) + ℓ_{2} (2 x_{1} - x_{2}) + ℓ_{3} - ℓ_{4} (5 x_{1} + 1), \leftarrow_{$} Z_{p}, ℓ_{3} \leftarrow_{$} Z_{p}, ℓ_{4} \leftarrow_{$} Z_{p} .$ 这相当于在上一个过渡博弈里作换元，用 $ℓ_{3}$ 表示 $r_{2} 。$ 到此为止，局部正确性已经提升为全局正确性， $ℓ_{1}$ 惟一满足 AKGS 求值正确性条件的数。

$H_{10}$

ctsksksk

密文、密钥应答方式
回应	正常	编程空间
回应	正常	一	二	三
$i s k_{1}$	$0, 0$	$1$	$0$	$0$
$i s k_{2}$	$ℓ_{2}, 0$	$0$	$0$	$0$
$i s k_{3}$	$ℓ_{3}, 0$	$0$	$0$	$0$
$i s k_{4}$	$ℓ_{4}, 0$	$0$	$0$	$0$
$i c t$	$1, x$	$ℓ_{1}$	$0$	$0$

标签计算方式为 $ℓ_{1} ℓ_{2} = μ ((2 x_{1} - x_{2}) (x_{3} + 3 x_{2}) + (5 x_{1} + 1) x_{4}) + ℓ_{2} (2 x_{1} - x_{2}) + ℓ_{3} - ℓ_{4} (5 x_{1} + 1), \leftarrow_{$} Z_{p}, ℓ_{3} \leftarrow_{$} Z_{p}, ℓ_{4} \leftarrow_{$} Z_{p} .$ 注意 $ℓ_{1}$ 和 $μ$ 独立，这是因为使坏者的查询满足“不允许解密”的限制，而 $μ$ 直接和算术公式相乘，后者满足 $(2 x_{1} - x_{2}) (x_{3} + 3 x_{2}) + (5 x_{1} + 1) x_{4} = 0 。$

思路整理

开始整理思路之前提一句，上述例子里的 $H_{10}$ 其实和诈和证明里的 $H_{2}$ 很类似，主要区别是：

正确的 $H_{10}$ 里除了 $ℓ_{1}$ 之外的标签是随机数；诈和的 $H_{2}$ 没有利用 $S i m$ 的特殊性质，很可能一个标签也无法正确设置。
正确的 $H_{10}$ 把 $ℓ_{1}$ 放在密文里，是可行的；诈和的 $H_{2}$ 里所有的标签都在密钥里，不可行。
正确的 $H_{10}$ 准备了足够的编程空间，过渡证明法得以完成；诈和的 $H_{2}$ 没有明显的编程空间。

现在来总结一下过渡博弈是如何递归生成的，递归过程针对一个中间节点 $g ，$ 满足如下不变式 (invariant)：

递归之前， $g$ 所有叶子都是正常状态，即标签函数位于 $i s k$ 里。
递归期间， $g$ 每个叶子对应的标签都暂时会被挪动到 $i c t$ 的空位中，大多数叶子会变成随机数，然后被挪回 $i s k$ 里。
递归结束时， $g$ 所有非最左叶子都具有随机标签且位于 $i s k$ 里，而最左叶子根据 $g$ 的局部正确性推算出来，位于 $i c t$ 的编程空间中。

递归算法也很简单：

若 $g$ 是叶子节点，则把对应标签从 $i s k$ 里挪到 $i c t$ 中一个未被占用的位置，然后返回。
若 $g$ 是非叶子节点，则分四步：
1. 对 $g$ 的左子节点 $g_{L}$ 递归，记 $g_{L}$ 最左叶子对应的标签是 $ℓ_{L} 。$
2. 对 $g$ 的右子节点递归，类似记 $g_{R}, ℓ_{R} 。$
3. 把 $g_{R}$ 的局部求值从乱码化算法规定的值改成随机数，这相当于不再考虑 $g_{L}, g_{R}$ 局部正确性，而是设置 $ℓ_{R} \leftarrow_{$} Z_{p}$ 并根据 $g$ 的局部正确性计算 $ℓ_{L} 。$
4. 把已经变成随机数的 $ℓ_{R}$ 挪回它的 $i s k$ 里。

现在摆在面前有三个问题：

递归步骤 3 正确（只是对博弈观念 [conceptual] 而非实质的改变）吗？
递归展开后有多少个基本步骤（即需要多少个过渡博弈）？
递归期间用到多少编程空间？

递归步骤 3 的正确性可以归纳证明，留作读者习题。记 $g$ 的乱码化规模为 $∣ g ∣ ，$ 可以归纳证明递归产生的过渡步骤数 $\leq 3 ∣ g ∣ - 2 = O (∣ g ∣) 。$ 至于编程空间，记公式树深度 $\leq d$ 时需要的编程空间 $\leq s (d) ，$ 跟踪递归步骤：

对于叶子节点， $d = 1, s (1) \leq 1 。$
对于非叶子节点， $d > 1 ：$
1. 左子节点的深度 $\leq d - 1 ，$ 递归左子节点时编程空间 $\leq s (d - 1) ，$ 结束时左子节点的最左叶子占用 1 个位置。
2. 右子节点类似，但要考虑左子节点的最左叶子已经占用了 1 个位置。
3. 最后的步骤会从 2 个位置退回 1 个位置。

因此 $s (d) \leq 1 + s (d - 1) ，$ 故 $s (d) \leq d 。$ 但还有一个问题是公式的深度可以有规模那么大，这样的话无论设置多大（多项式级别）的编程空间，似乎使坏者总是可以找到更大规模和深度（但仍然是多项式级别）的算术公式，让证明失败。好消息是我们有如下定理：

算术公式并行化（算术公式树平衡化）Bre74 BCE91 存在常数 $C$ 和高效算法，可将规模为 $S$ 的算术公式转换为深度 $\leq C + C lo g_{2} S = O (lo g S)$ 的等价算术公式（所定义的函数相同）。注意得出公式的规模必然 $\leq 2^{C} S^{C} = S^{O (1)} 。$

如果我们设置编程空间大小为 $⌈ C (1 + λ) ⌉ ，$ 只要在生成密钥前进行平衡化，就可以对（起初）规模 $\leq 2^{λ}$ 的公式证明安全性。由于假设使坏者运行时间总是 $λ$ 的多项式级别，故 OK。

本篇结语

这一篇里我解释了上一篇里证明的诈和之处，并给出了当时想到的第一个解决方案——根据算术公式 AKGS 乱码化、求值的递归过程进行递归逐步模拟。这部分在“冰冷美丽”的论文中没有详细记载，希望这篇文章能留下“火热思考”的印记。下一次我会接着这个话题谈后来的新发现。

参考文献

BCE91 ↩ Nader H. Bshouty, Richard Cleve, and Wayne Eberly. Size-Depth Tradeoffs for Algebraic Formulae. In 32nd FOCS, pages 334–341. IEEE Computer Society Press, October 1991.

Bel98 ↩ Mihir Bellare. Practice-Oriented Provable-Security (Invited Lecture). In Eiji Okamoto, George I. Davida, and Masahiro Mambo, editors, ISW’97, volume 1396 of LNCS, pages 221–231. Springer, Heidelberg, September 1998.

Bre74 ↩ Richard P. Brent. The Parallel Evaluation of General Arithmetic Expressions. J. ACM, 21(2):201–206, April 1974.

Dam07 ↩ Ivan Damgård. A “proof-reading” of Some Issues in Cryptography (Invited Lecture). In Lars Arge, Christian Cachin, Tomasz Jurdzinski, and Andrzej Tarlecki, editors, ICALP 2007, volume 4596 of LNCS, pages 2–11. Springer, Heidelberg, July 2007.

Fre61 ↩ Hans Freudenthal, editor. The Concept and the Role of the Model in Mathematics and Natural and Social Sciences, Springer Science and Business Media B.V., 1961.

Fre02 ↩ Hans Freudenthal. Didactical Phenomenology of Mathematical Structures. Kluwer Academic Publishers, 2002. Quote from A Look Backward and a Look Forward. See https://doi.org/10.1007/0-306-47235-X.

KM07 ↩ Neal Koblitz and Alfred J. Menezes. Another Look at “Provable Security”. Journal of Cryptology, 20(1):3–37, January 2007.

KW19 ↩↩ Lucas Kowalczyk and Hoeteck Wee. Compact Adaptively Secure ABE for

N C^{1}

from

k

-Lin. In Yuval Ishai and Vincent Rijmen, editors, EUROCRYPT 2019, Part I, volume 11476 of LNCS, pages 3–33. Springer, Heidelberg, May 2019.

LL20 ↩↩ Huijia Lin and Ji Luo. Compact Adaptively Secure ABE from

k

-Lin: Beyond

N C^{1}

and Towards

N L

. In Anne Canteaut and Yuval Ishai, editors, EUROCRYPT 2020, Part III, volume 12107 of LNCS, pages 247–277. Springer, Heidelberg, May 2020.

属性加密：修复诈和

前情提要

诈和揭秘

递归模拟算术公式

具体例子

Exp1-ABE​

H1​

H2​

H3​

H4​

H5​

H6​

H7​

H8​

H9​

H10​

思路整理

本篇结语

参考文献

$E x p_{1-ABE}$

$H_{1}$

$H_{2}$

$H_{3}$

$H_{4}$

$H_{5}$

$H_{6}$

$H_{7}$

$H_{8}$

$H_{9}$

$H_{10}$