我发现当我的生活充实的时候就有有趣的 blog 可以写!因为一忙起来,就要忙里偷闲,然后就会胡思乱想,然后就可能有有意思的东西。
我在实现一个算法,于是忙里偷闲,于是胡思乱想。有一个数列(算法用掉的资源数目)是归纳定义的:a0=a1=0,a2n=4an+4,a2n+1=2an+2an+1+4.当然计算机科学家喜欢的写法是 an=4an/2+Θ(1),用主定理一下就知道 an=Θ(n2)。虽然在实际实现的过程中用不到这个数列的具体数值,但是我还是对这个数列很感兴趣,比如,我可能希望在算法开始之前预估(upper-bound 之)这个数字。
写程序算这个数列的前 1000 项,并计算 n−2an,可以发现这个比值在 1.3 到 1.5 之间徘徊,而且从未到达 1.5。容易猜想 n−2an≤1.5,实际上我认为 1.5 应该是这个比值的上极限。
那么怎么验证这件事情呢?(理论计算机科学家的毛病?总想证明!)一个简单的思路是去证明 an≤1.5n2。有一个方法叫做归纳法,有一个方法叫做加强命题,有一个方法叫做待定系数。直接归纳做不了,自然地想到加强命题,加强到什么样子呢?那就待定系数决定好了。就是这么鸡贼!实际上这个方法我用过不少次,但是从来没有把这种组合明确说出来;明确说出来之后觉得好猥琐……
考虑归纳证明 an≤An2+Bn+C,随便胡写一点,可以发现选择的数要满足不等式组A+B+C2nB+3C+4A+(2n+1)B+3C+4≥0,≤0,≤0,其中 n 跑遍正整数,这等价于A+B+C2B+3C+4A+3B+3C+4B≥0,≤0,≤0,≤0,在这个条件下最小化 A,这是一个线性规划问题,算出来 A=2,B=−2,C=0 是最优解。
结论强度不够啊!
嗯,这时候需要一点点小技巧——所谓“前有限项没必要关心”。简单来说想要得到渐近的 bound,我们可以从下标较大的地方开始。如果从第 2n 项(或第 2n+1 项)开始归纳,我们只需要不等式对 n,⋯,2n−1(或外加 2n 这项)这些项成立。归纳推理用到的不等式也有所放松。
经过简单的尝试,如果从 a4 开始用归纳,需要满足的不等式组是4A+2B+C9A+3B+C4B+3C+4A+5B+3C+4B≥4,≥12,≤0,≤0,≤0,最优解是 a=23,b=−21,c=−1。
Tada! 这就验证了 n−2an≤1.5,不过具体是不是上极限暂时还不知道。
现在我想调查一下:你觉得这种操作常见吗?还是说这是一个骚操作?回复或者通过别的渠道告诉我 😁
另外,你可以 点击这里获取小甜点。
最后作为小甜点,我们求解一下通项公式。这个过程和结果都比较简单,而且适合用电脑算。根据递推式和首项,an+1 的普通幂级数生成函数 f(x) 满足方程f(x)=2(x+1)2f(x2)+1−x4x.两侧同乘 (1−x)2logx 再叠加(我懒得验证形式表达式这样做对不对,待会儿说这事儿),得到f(x)=(1−x)21n=0∑∞2n+2x2n(1−x2n)所以==an+1k=0∑t(n+1−2k)2k+2−k=0∑t−1(n+1−2k+1)2k+24(n+1)2t−31(8⋅4t+4),其中 t=⌊log2n⌋。经过验算这个表达式是正确的(通过前 1000 项验算,并检查该级数符合之前的方程),因此之前我没有验证形式表达式运算合理性的事情,就请大家忘记吧,这个结果是我观(瞪)察(眼)得到的(所谓“注意到”)。
另,可以解答刚刚的一个遗留问题了:n−2an 的极限点集是 [34,23],我猜的上极限是对的。考虑 an+1=r−12t→∞,有(n+1)2an+1=4r−38r2+o(1),因此 n−2an 的极限点集就是 {4r−38r2∣r∈(21,1]} 的闭包。
聪明反被聪明误
把这篇博文传出去给一些朋友看,胡波有一个很聪明的做法。先上一个图,毕竟“数形结合百般好,隔裂分家万事休”:
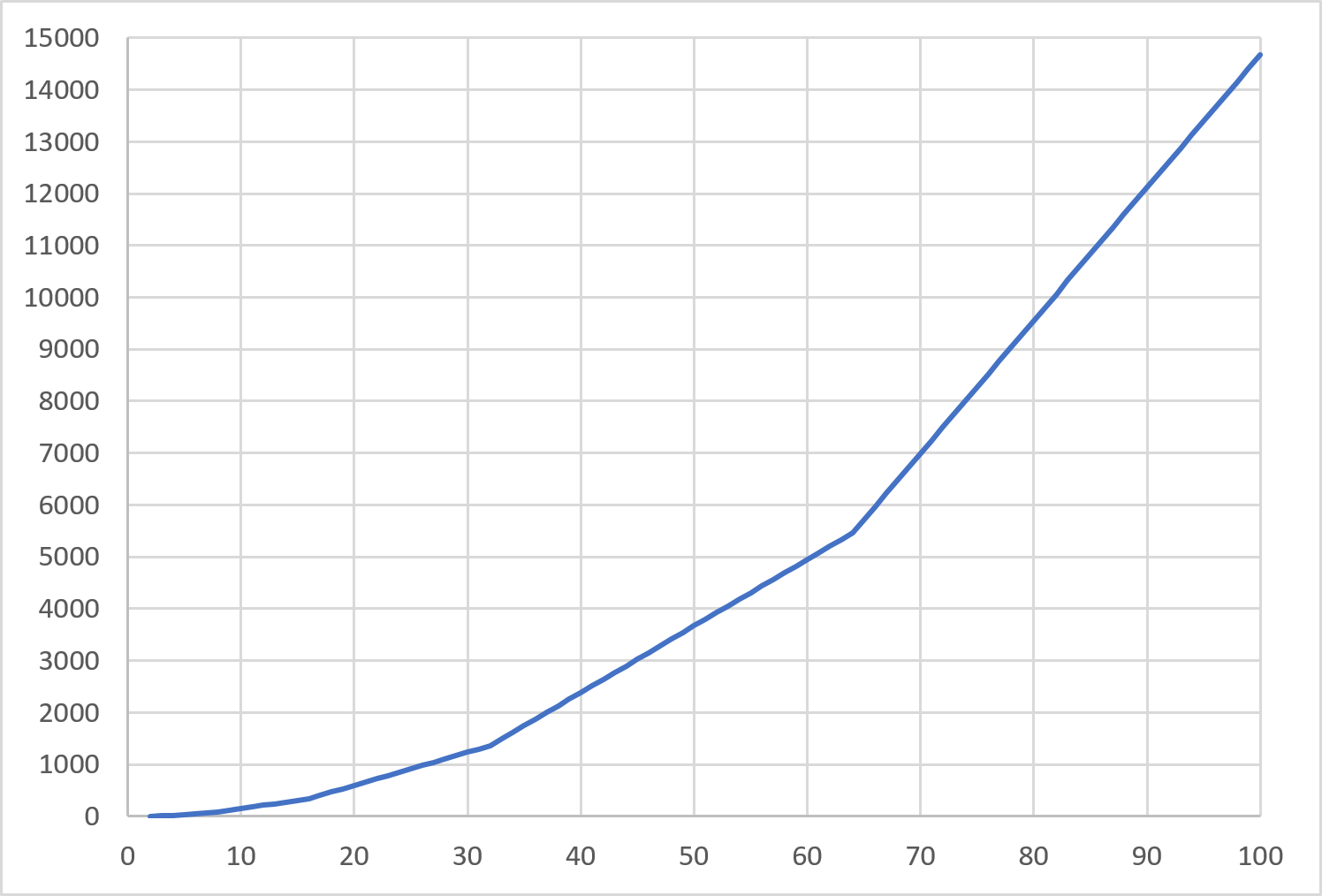 数列第 2 到第 100 项
数列第 2 到第 100 项
这个图暗示了两件事儿:
胡波注意到 a2n+1=21(a2n+a2n+2)。如果我们按照这样的方法计算:
- 从只有一项 a1=0 开始;
- 把当前所有项乘 4 再加 4,得到更大范围的偶数项;
- 把更大范围里的奇数项通过相邻两项的平均数算出来;
- 现在有结果的范围扩大了一倍,回到第 2 步继续;
则容易用归纳法得到:an 在 2t≤n≤2t+1 范围内是 n 的一次函数,对所有自然数 t。因此只要计算 a2n 的通项自然就得到了 an 的通项,用常用技巧把递推式变成方便求和的样子4−n−1a2n+1=4−na2n+4−n,反复运用该递推式有a2n=4nk=0∑n−14−k=34(4n−1),于是得出结论。
同学的差分大法
我的同学 MT 表示可以考虑数列 dn=an−an−1,这样可以得到 dn=2d⌈n/2⌉,于是 dn=2⌈log2n⌉+2,后面略。他还发现了我的一个笔误。以下是我们并不有趣的微信对话。
8 月 10 日更新:实际上该方法(作差分)是和普通幂级数生成函数里的解法不谋而合的,因为对普通幂级数生成函数乘 (1−x) 就是作差分;在我的解法里,我做了两次差分,这就会得到一个“经常是 0,在 2 的乘方下标附近不是 0”的数列,而求两次前缀和等同于和 an=n(或者下标有个什么错位之类的)作卷积。
09:50
Typo
A=3/2
shit
这tm怎么发现的
你看了最后那部分了么
看了啊
分段直线
是很显然的啊
并不觉得显然🤣
09:51
我已经忘记怎么思考了
因为之前的方法(生成函数)不需要思考
我不是评论了嘛
作差分,起飞
每次下标是一起减少目前下标一半取整🤣
然后我觉得您的方法或许可以扩展到 /3 的情况
对啊,然后就等于log取整
比如用 omega 组合
系列需要雕琢一下但是渐进3/2n^2还是很好做的
*细节
09:57
<3/2我依然站待定系数归纳
至于limsup……反正每个神仙最后都求出通项了

用差分的优势在于一眼看出这是啥…



请启用 JavaScript 来查看由 Disqus 驱动的评论。