属性加密（番外）：分段安全性的故事
这一篇是我的 2019 年科研“属性加密”系列番外篇，记录一些关于（特殊）分段安全性的故事。这一篇的风格相较主系列更轻松活泼（肯定有人要吐槽我对“轻松活泼”的定义），比如去掉了繁复的导航按钮，减少了公式。另外这一篇也加上了“数学”的标签，大概是因为很多这里考虑的问题的密码学价值不大，更像是线性代数的游戏？
Blog entries with tag ‘Maths’
- Math
- 数学
How many cells can a planar curve touch?
The obvious answer to this little geometry puzzle is 3/√2, but can you prove it?
A series about iterated cosine
Just some random proposition found on Twitter.
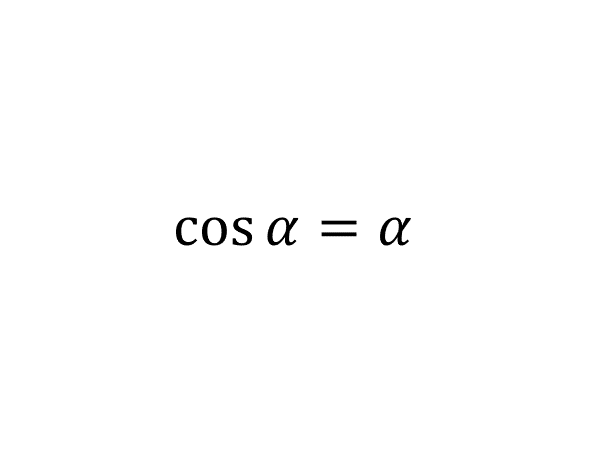
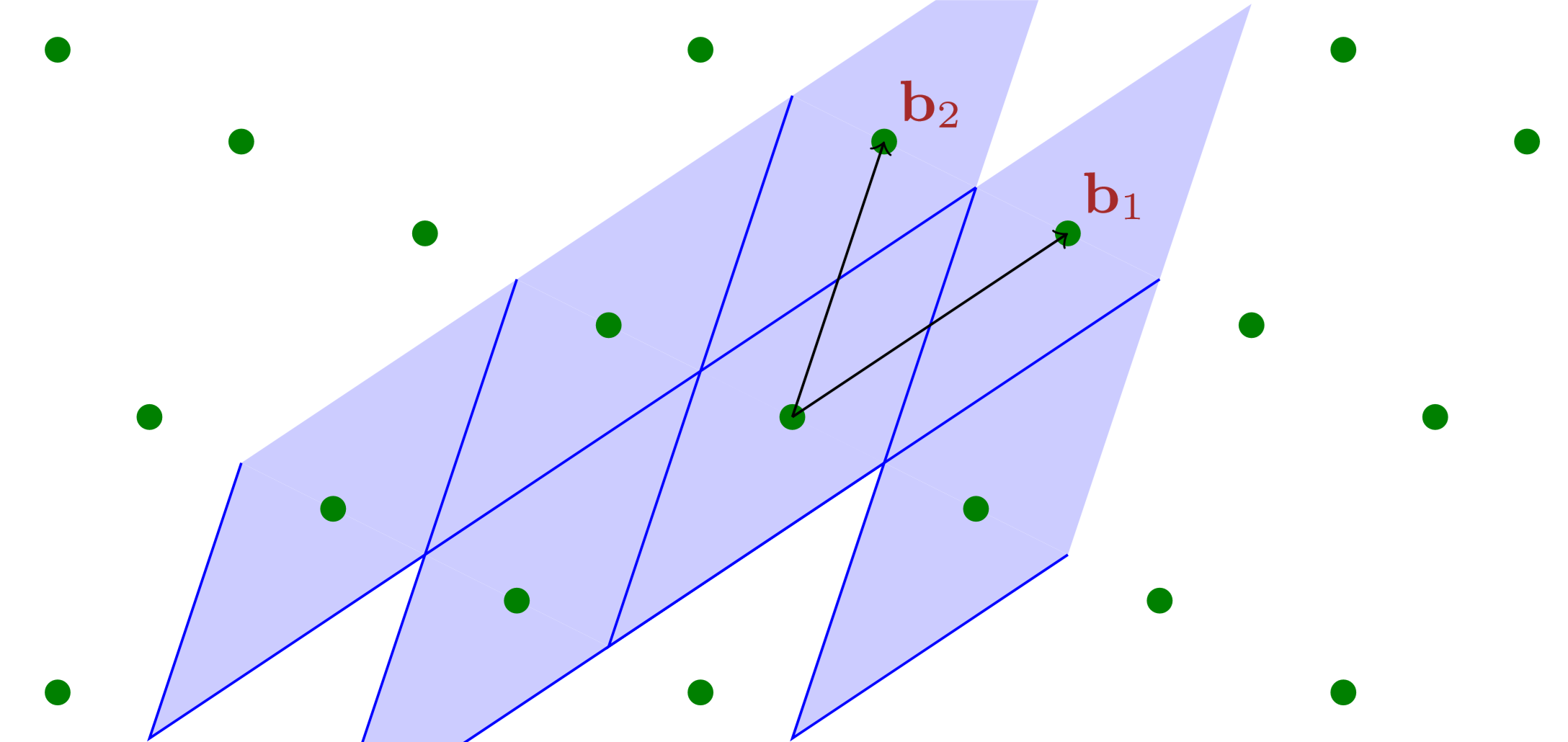
Notes for UMich EECS 598 (2015): Homework 2
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for homework 2.
Notes for UMich EECS 598 (2015): Homework 1
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for homework 1.
Notes for UMich EECS 598 (2015): Lecture 1
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for lecture 1, mathematical background.
NP 验证式的答题风格
神来之笔一般的答案背后是草稿纸上的一通狂算，考试要看的是神来之笔，但其实一通狂算里的思路更有价值。关键词：十一学校、抄答案、“注意到”、“草稿”。
Red envelopes
WeChat has this function to distribute red envelopes of random amount of money. The natural question to ask is how to sample the amount of money each person who opens the envelope should receive.
谈“理想”和其他
理想（ideal）是出现在抽象代数（更特别地，环论）中的一类对象，其命名很有渊源。之前我只知道这个名字来源于一位数学家研究惟一分解时引入的“理想数”（该研究的思路和一般化最终形成了现代数学语言中“理想”的定义），但是具体的细节不是很明白；最近在阅读基于格（lattice）的密码学的内容，其中提到了环上的格（ring lattice），其中提到了理想格（环的一个子集，同时满足格和理想的要求），好奇心一发不可收拾，读了一些数学历史故事，对“理想数”加深了认识，记录下来以飨观众。文章最后讨论了“理想数”这个翻译的不达意之处。
Nyuwa mends the epigraph
Nyuwa, the mother goddess of Chinese mythology, mends the sky according to an ancient Chinese legend. Today, Nyuwa is asked to mend the epigraph of a continuous function over an open set so that the function becomes convex. What can we say about this?
In memory of a nightmare: solving linear equation over PID
I had a maths-related nightmare that (initially) was concerned about counting solutions of a linear equation modulo M with integral coefficients. Though the whole detail of the dream cannot be written down due to privacy reasons, at least I can write a simple introduction on solving this specific problem here. Update: An error in the original solution has been corrected. Another update the same day: The original solution is correct.
A note on finitely generated/related/presented groups
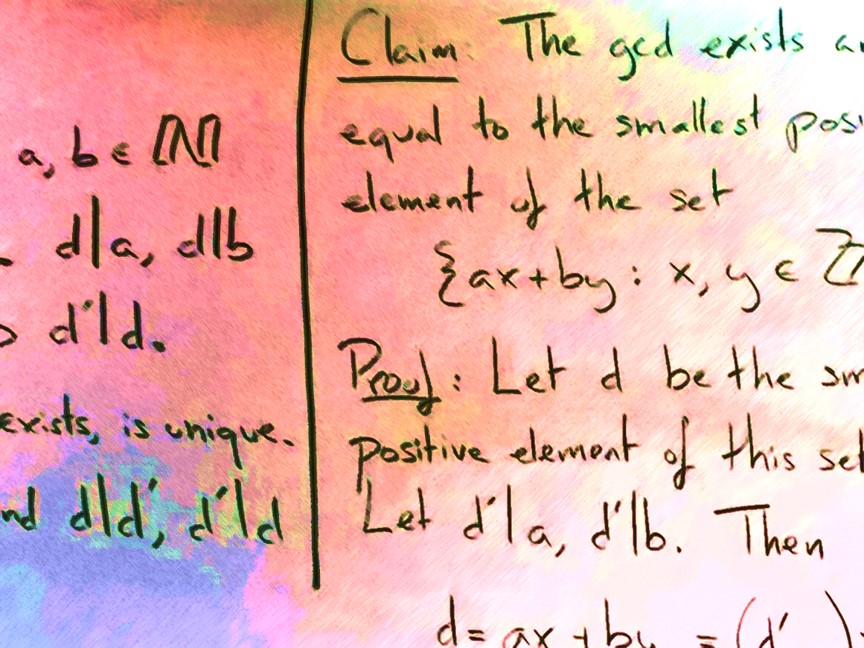
Group presentation is a method to express groups as a quotient of a free group and a normal subgroup. In a presentation, there are generators and relators, and the presentation yields a ‘minimalist implementation’ of these generators and relations. Some cases of special interests are finitely generated/related/presented groups. From the definition, finite generation + finite relation is not linguistically equivalent to finite presentation. There has been some discussion on the relation of the three properties for several other algebraic structures. This entry proves that finite generation + finite relation implies finite presentation for groups.
What goes wrong when arrows are reversed in the diagrams for direct product/sum universal properties?
I’m taking an algebra course and regaining my algebra sense (non-sense?). Familiar to us is that direct products [resp. sums] of groups [resp. abelian groups] possess their versions of universal properties. When reviewing these things, I went curious on what would go wrong if the arrows were reversed. Let’s try and see.
微博校园发的一个阴（博）谋（弈）论题目
微博校园发了一个转得都“变质”的考试附加题照片——还有可能是 PS 的！那些字真的跟纹身刚刚纹上去的时候一样，底下还泛红。我把这个题做了一做，又苦于最近没什么新的博文主题，就暂且写一篇这个罢了。
The Code Book (Simon Singh) 读书笔记
操作系统课中讲安全的一节是代课老师上的，期间他推荐了 The Code Book (Simon Singh) 这本书，说是讲密码学历史的。我对密码学感兴趣，就读了一读，并照“不动笔墨不读书”的原则，记了读书笔记，发表出来以飨观众。
Find a 0-1 matrix whose determinant is a given integer
Jinhao Zhao was making up problems for some OIers. Let’s see this maths problem!
Rethinking base ‘conversion’
Base conversion is the conversion between notations of number, and NOT the numbers themselves. I discuss a common mistake on methods of base conversion, and a common mistake in thinking about ‘base conversion’ in computer programs.
Chit-chat on Lagrange’s four-square theorem
Lagrange’s four-square theorem is a beautiful result in number theory. However, to the best of my knowledge, I haven’t encountered it often in theoretical computer science. Today’s entry discusses two interesting stories related to this theorem.
Is the pattern you found persuasive?
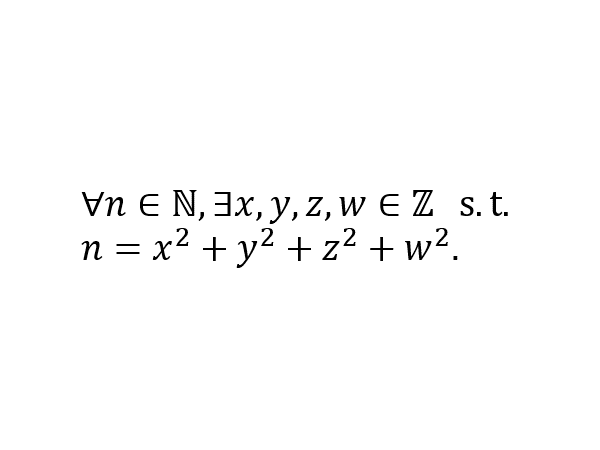
Starting from the classic puzzles of finding patterns in a sequence, this entry explores the framework to define persuasive patterns. The framework is found to be quite self-contained in the sense that it is ‘asymptotically invariant’ to the choice of ‘language of expression’. The only short-coming of this framework is that it works only for computable sequences, yet the process of pattern discovery is uncomputable.
Of elementary general terms
In this entry, I discuss a pathological construction of general terms of a class of integer-valued sequences with the widely accepted concept of ‘elementary functions’. The idea here is to simply ‘concatenate’ the integers in a real number, then extract the appropriate digits for each term. It turns out that this definition characterises the elementariness very well (note that the definition is also self-referencing). The extended inspection leaves a problem open: Are all integer-valued sequences elementary? Update: The question is solved with an affirmative answer.
Mean value theorem and heuristics from differential equation
In this entry, I discuss a kind of widely posed exam problems for elementary calculus learners. It concerns a technique of application of (differential) mean value theorems. Specifically, a class of such problems can be solved dogmatically if the equation to prove resembles a ‘factorisable’ linear differential equation.
关于代数数的一段笔记
我学习过程中一些关于代数数的说明。
随机过程习题课见闻二则
去听习题课并不是为了听讲习题，而是为了混参与分数（虽然我相信这个课不用参与分数也可以拿很高的分）。虽然，仍然有两则有趣的见闻以飨观众。
鸡贼地 bound 一个数列
我发现当我的生活充实的时候就有有趣的 blog 可以写！因为一忙起来，就要忙里偷闲，然后就会胡思乱想，然后就可能有有意思的东西。（已更新）
Of Kerckhoffs’ principle
Let me explain the classic idea that ‘the algorithm of a crypto system should be considered and made public’ to you. Particularly, I will discuss what it means by ‘crypto system’, which tells us what information should be no secret at all.
数学文字中的“一般”
数学文字中有很多“一般”，例如“一般地”、“不失一般性”，还有“特别地”等说法，它们的意思和日常中的“一般来说”可大不相同。
Make the rows banded if and only if there are at least 4 rows
A practical problem I encountered in 2016, which I insisted on implementing with pure CSS as long as it was possible. At first it was solved with mathematical logic tricks but later it turned out there was a much simpler solution.
关于 6÷2(1+2)
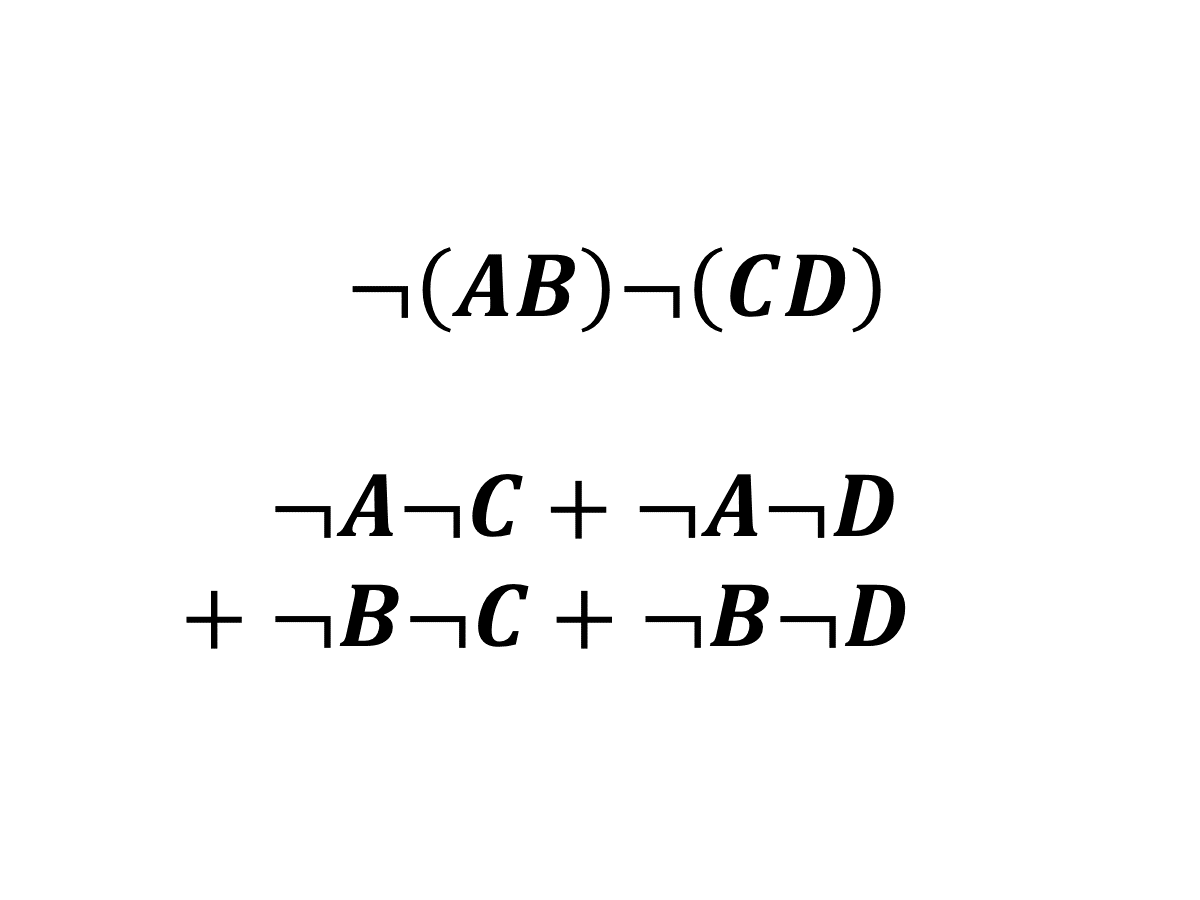
我倾向于认为答案是 1。
