What goes wrong when arrows are reversed in the diagrams for direct product/sum universal properties?

I’m taking an algebra course and regaining my algebra sense (non-sense?). Familiar to us is that direct products [resp. sums] of groups [resp. abelian groups] possess their versions of universal properties. When reviewing these things, I went curious on what would go wrong if the arrows were reversed. Let’s try and see.

Correct Version of Universal Properties

Direct Sum of Abelian Groups

Let ${\left(A_i\right)}_\idxi$ be a non-empty family of abelian groups and $A=\bigoplus_\idxi{A_i}$ their direct sum. Let $\eta_i:A_i\to A$ be canonical injections for all $\idxi$. 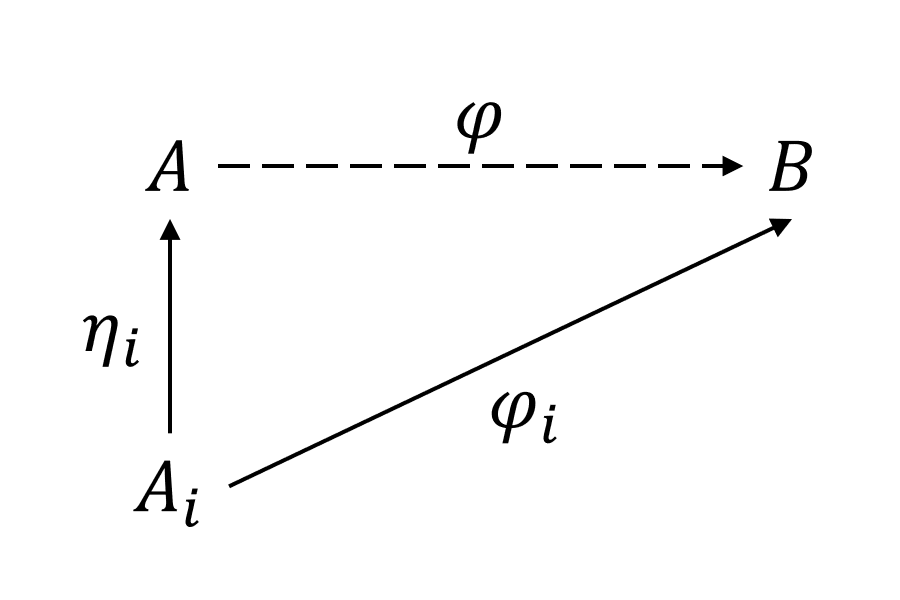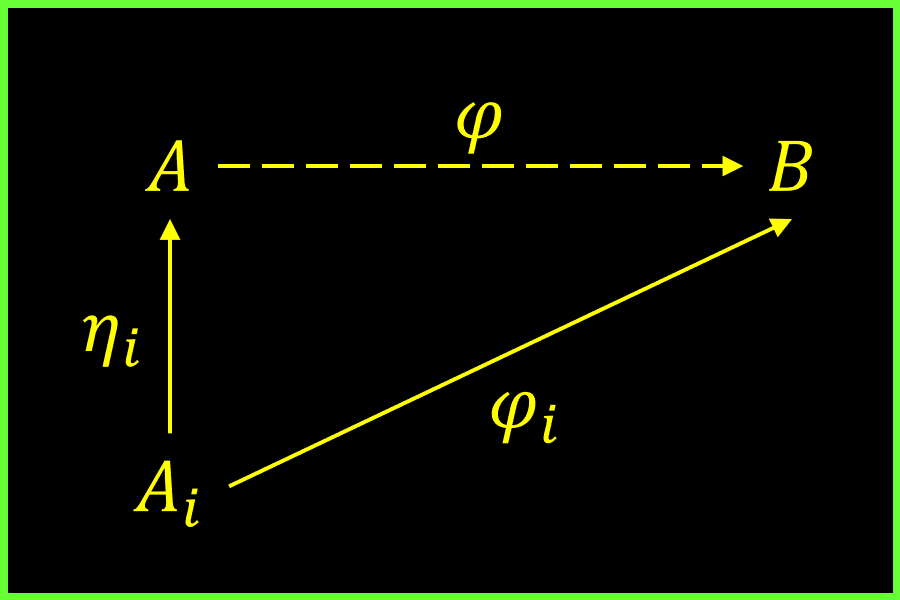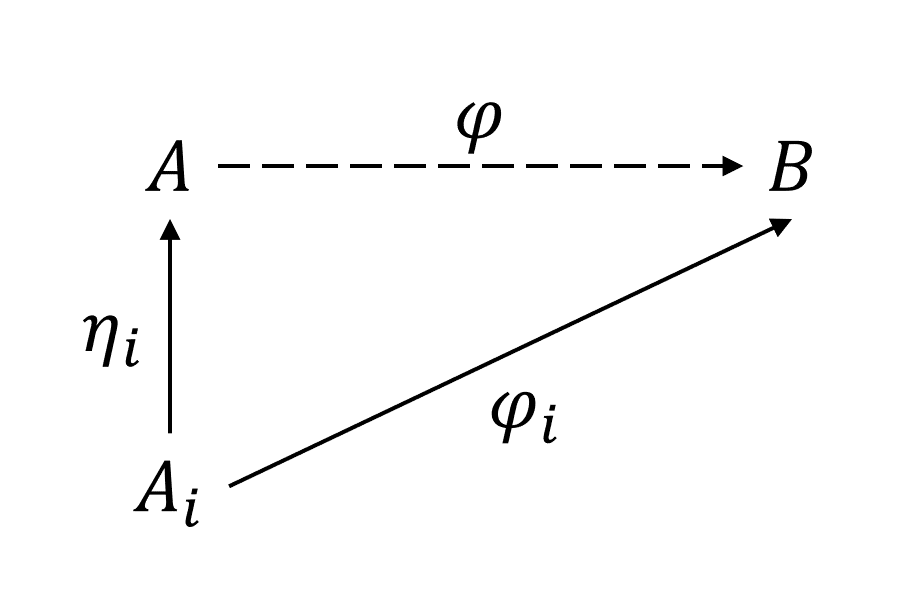For all abelian group $B$ and a family of homomorphisms $\varphi_i:A_i\to B,\forall\idxi$, there exists a unique homomorphism $\varphi:A\to B$ such that $\varphi\eta_i=\varphi_i$ for all $\idxi$, i.e., the following diagrams commute for all 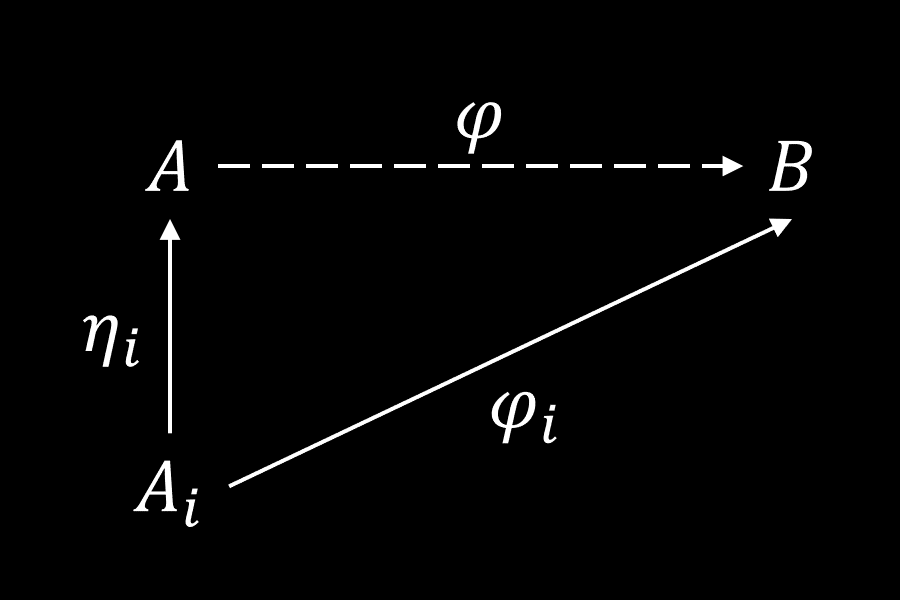$\idxi$: This homomorphism is $\displaystyle\varphi\left({\left(a_i\right)}_\idxi\right)=\sum_\idxi^x{\varphi_i\left(a_i\right)}$.

Direct Product of Groups

Let ${\left(G_i\right)}_\idxi$ be a non-empty family of groups and $G=\prod_\idxi{G_i}$ their direct product. Let $\pi_i:G\to G_i$ be canonical projections for all $\idxi$. 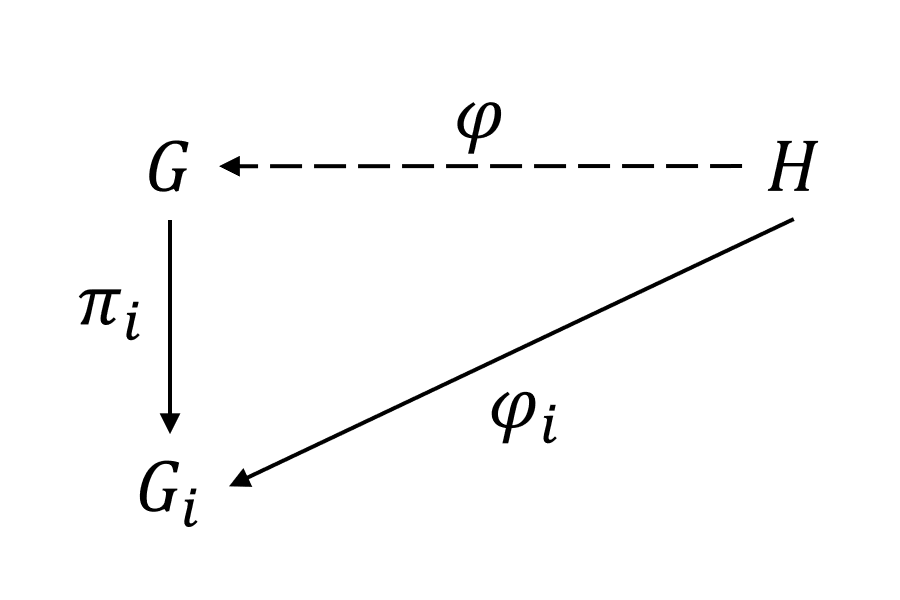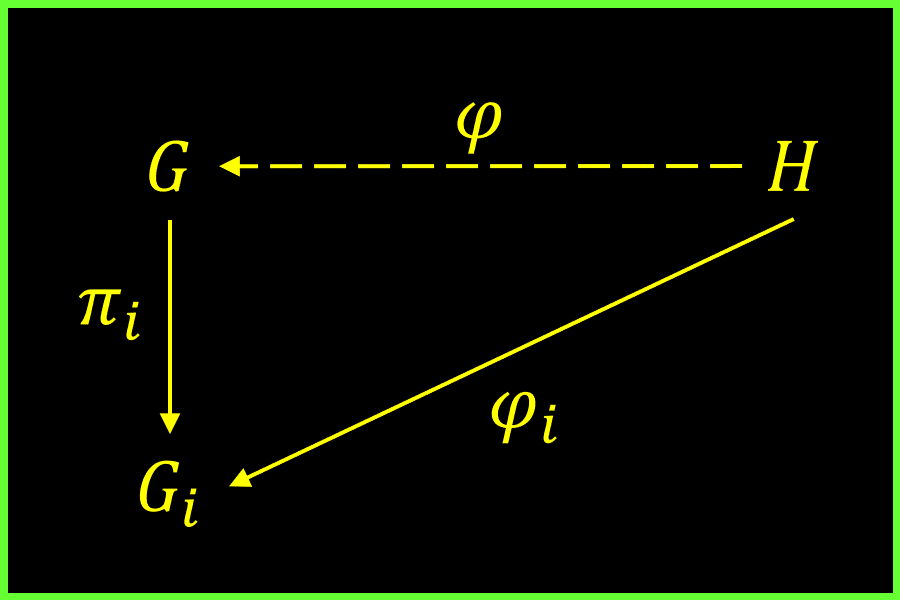For all group $H$ and a family of homomorphisms $\varphi_i:H\to G_i$, there exists a unique homomorphism $\varphi:H\to G$ such that $\pi_i\varphi=\varphi_i$ for all $\idxi$, i.e., the following diagrams commute for all 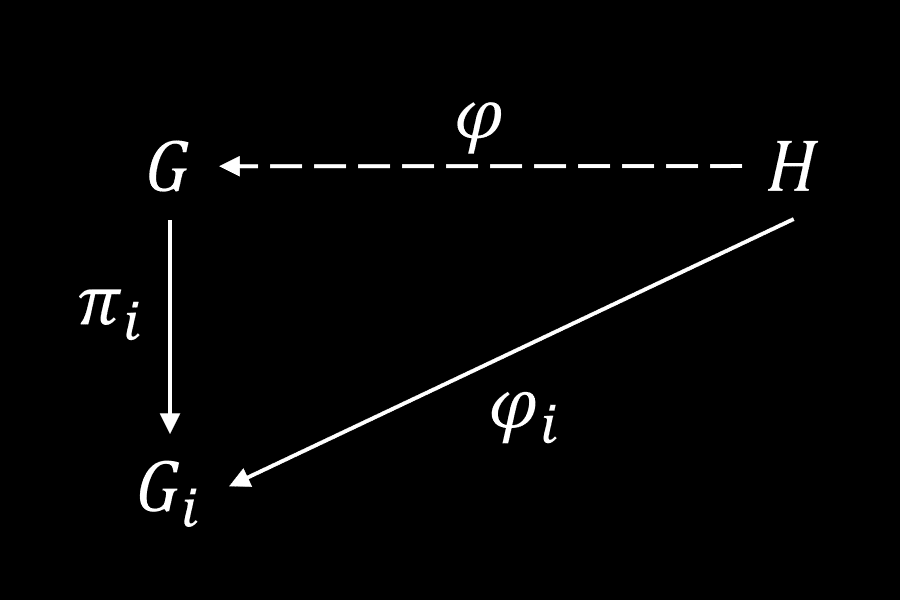$\idxi$: This homomorphism is $\displaystyle\varphi\left(h\right)={\left(\varphi_i\left(h\right)\right)}_\idxi$.

Incorrect Version of Universal Properties

We now explore what will go wrong if the arrows are reversed in the above diagrams. All symbols not redefined (or requantified) are assumed to have the same meaning as defined above.

⊕ for Π Properties

We still confine ourselves to abelian groups. Reversing the arrows means that for any abelian group $B$ and a family of homomorphisms $\varphi_i:B\to A_i$, we can induce a unique homomorphism $\varphi:B\to A$ such that $\pi_i\varphi=\varphi_i$. The homomorphism in imagination might not exist.

For all $a\in A$, there exists a finite subset $\mathcal{J}\subseteq\mathcal{I}$ such that $\pi_i\left(a\right)=0$ for all $i\in\mathcal{I}\setminus\mathcal{J}$. Since the image of the induced homomorphism must be in the direct sum, this puts a restriction on what family of $\varphi_i$ one can choose. For example, consider $\mathcal{I}=\mathbb{N}$, $B=A_i=\mathbb{Z}$ and $\varphi_i=\id_\mathbb{Z}$. The image of $1$ under the imaginary induced $\varphi$ would not lie in the direct sum.

If such a homomorphism can be induced, it will be unique. Such a homomorphism exists if and only if the induced one for direct product maps only into the direct sum, and in that case, the induced homomorphism is simply the one for the direct product.

Π for ⊕ Properties

Existence

Under general group setting, the homomorphism in question might not exist. The factor groups are naturally embedded as disjoint normal subgroups of the product (i.e., the internal direct product decomposition). We use that to find a counterexample.

Let $\mathcal{I}=\left\{{1,2}\right\}$, $G_1=G_2=H$ and $\varphi_i=\id_H$. If an induced homomorphism $\varphi$ exists, we know that for all $x,y\in H$, $\ProdSumFail$ which means $H$ must be abelian. Picking a non-abelian $H$ yields a counterexample.

Existence (Abelian)

The homomorphism in question might not exist even if we are working exclusively with abelian groups. For abelian groups, one can always induce the homomorphism from the direct sum to the codomain, which can be any possible such homomorphism. The question is thus equivalent to wheher arbitrary homomorphism from the direct sum to some codomain can be extended to one from the direct product. This turns out to be equivalent to whether the direct sum is a direct summand of the direct product (see remarks).

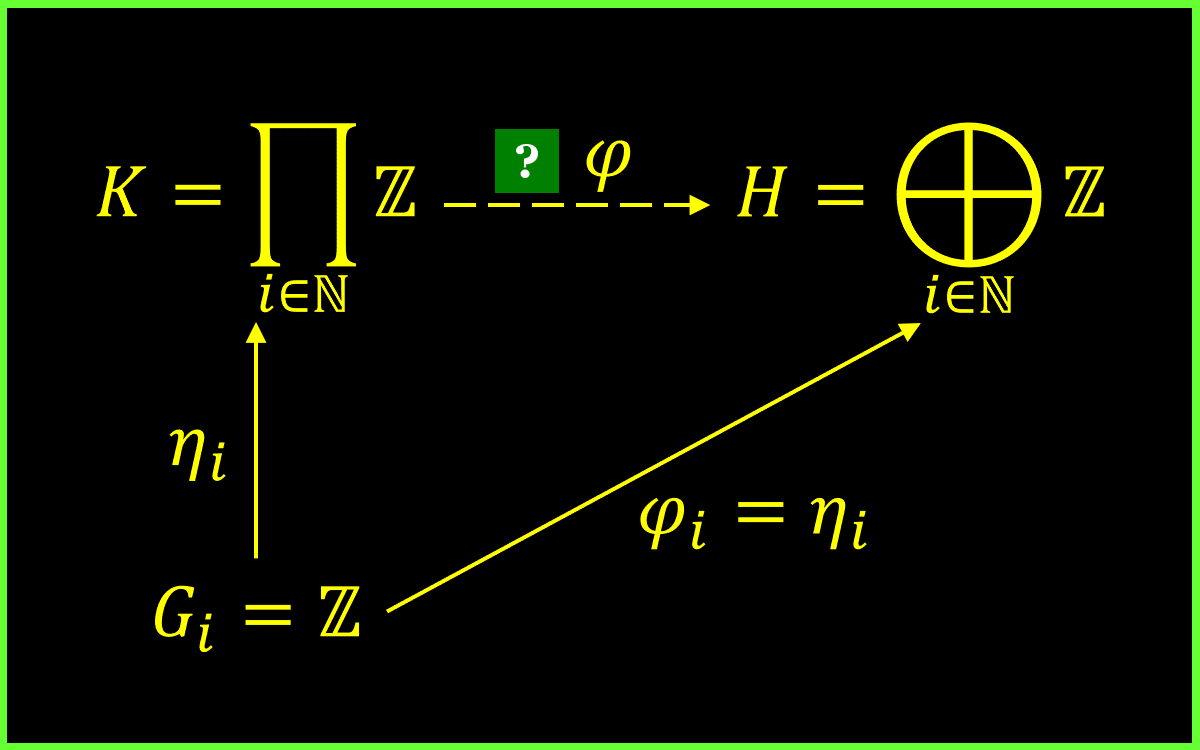
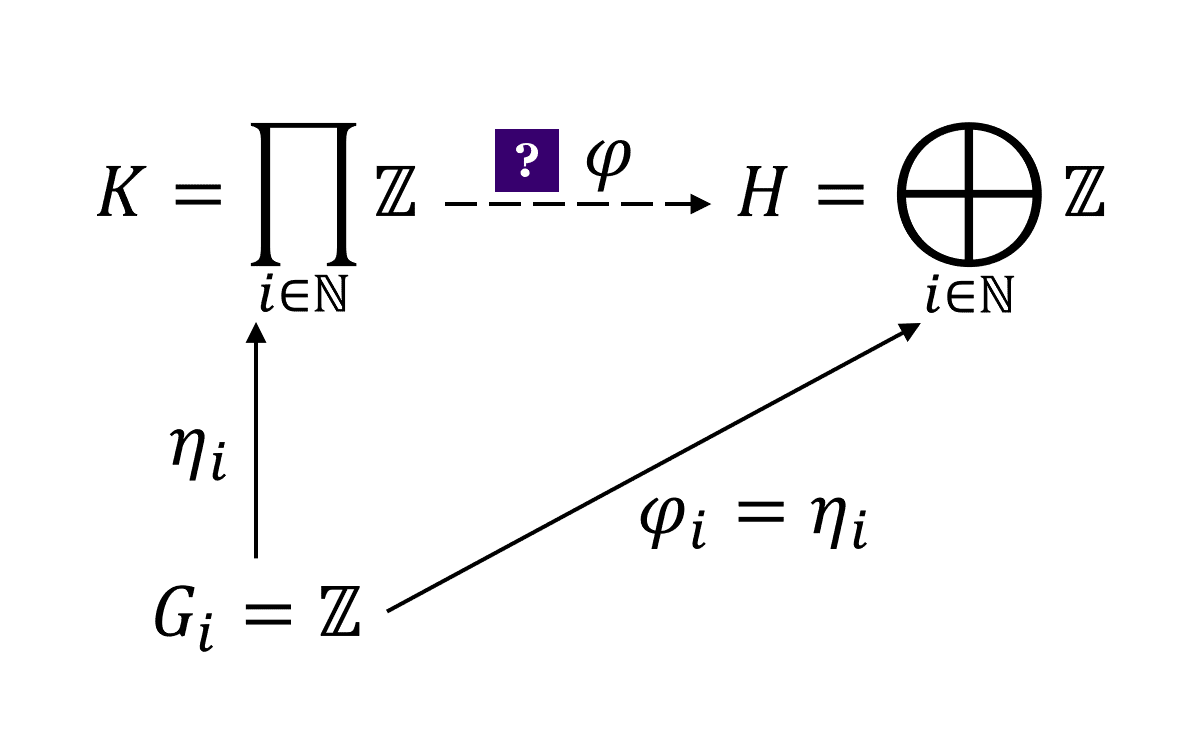
We have chosen the identity map for the previous two counterexamples. This time, it involves using the direct sum itself as the codomain. Let $\mathcal{I}=\mathbb{N}$, $G_i=\mathbb{Z}$, $\displaystyle H=\bigoplus_\idxi{G_i}$, $\displaystyle K=\prod_\idxi{G_i}$ and $\varphi_i=\eta_i$. Does there exists some $\varphi$ such that the following diagrams commute? 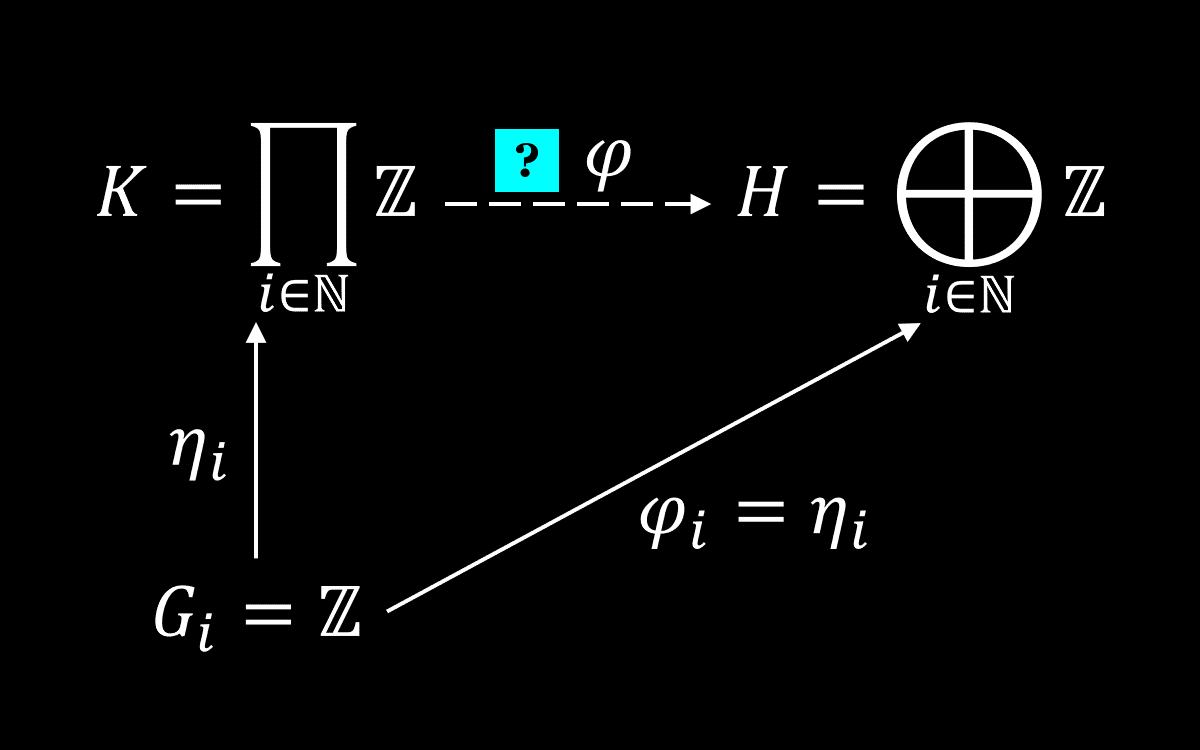The answer is no. We prove by contradiction. Assume yes instead, by the universal property of direct sum of abelian groups, we have ${\left.\varphi\right|}_H=\id_H$. This means $x-\varphi\left(x\right)=0$ for all $x\in H$. Now define $\MultipleSeq$ Since $x_0\notin H$ and $\varphi\left(x_0\right)\in H$, we have $y_0\neq 0$. Moreover, $x_0-2^nx_n\in H$, therefore $y_0=2^ny_n$. This contradicts the fact that $y_0$ has a non-zero integral coordinate.

Professor Goodearl suggests another counterexample. Consider $\displaystyle A=\prod_{p\text{ prime}}{\mathbb{Z}_p}$, then $\displaystyle T\left(A\right)=\bigoplus_{p\text{ prime}}{\mathbb{Z}_p}$ and $T\left(A\right)$ is not a direct summand of $A$. (Again see remarks for equivalence of direct summand and homomorphism extension.)

Uniqueness (Abelian)

Suppose that there exists an induced homomorphism for the reversed version of universal property for direct sum of abelian groups. How do we know whether the induction yields a unique homomorphism? If not, how can we describe the possible inductions?

For abelian groups, Professor Goodearl points out that one can study the difference between two induced homomorphisms.

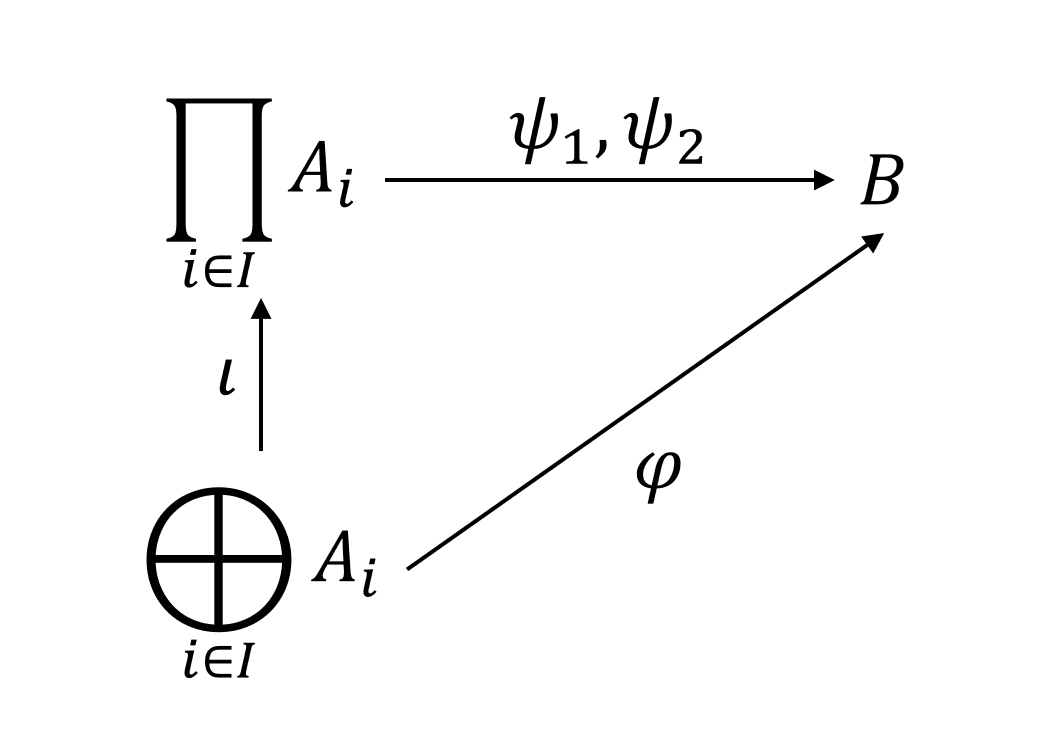
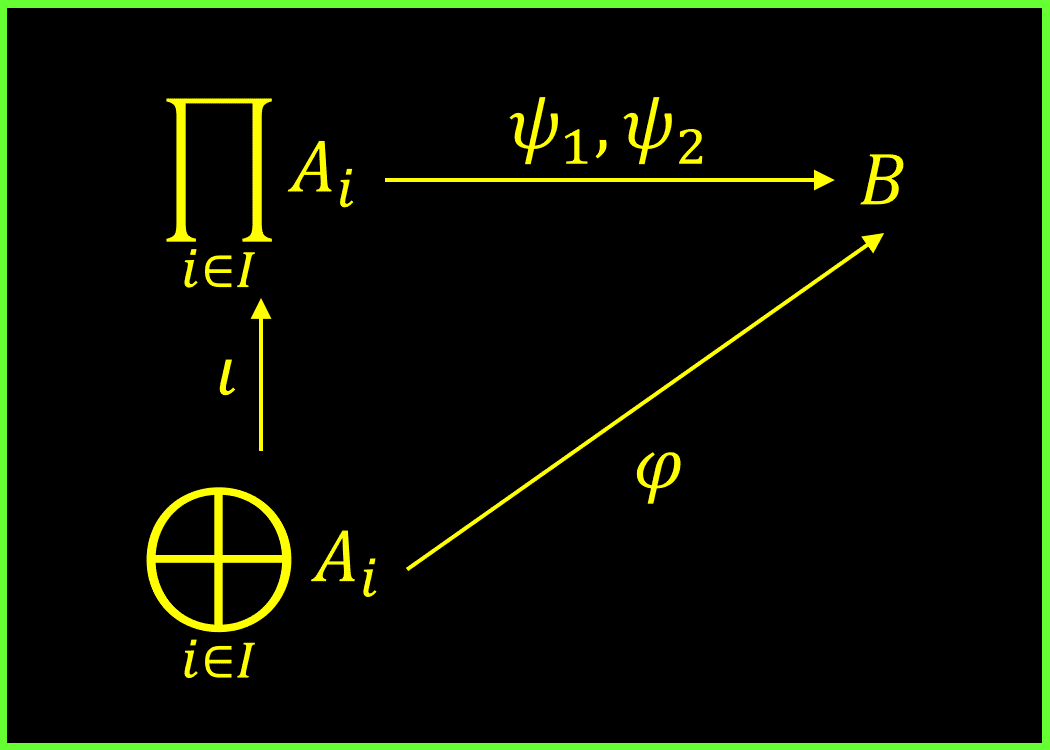
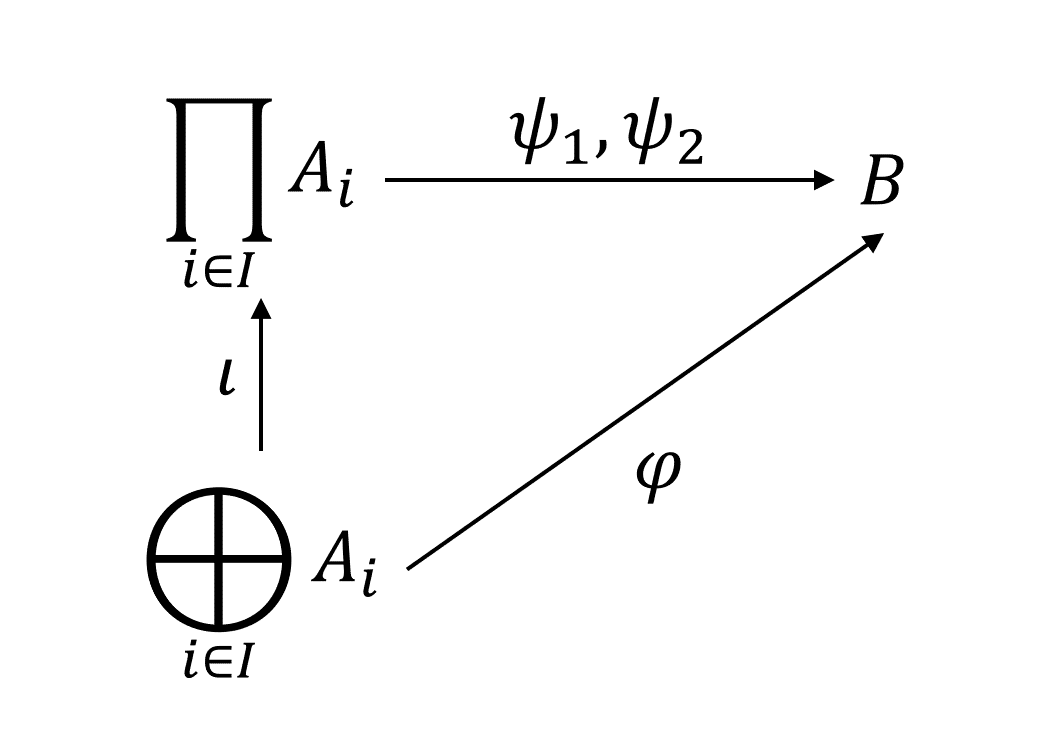
Given an abelian group homomorphism $\displaystyle\varphi:\bigoplus_\idxi{A_i}\to B$, consider two homomorphisms $\psi_1,\psi_2$ that make the following diagram commute: 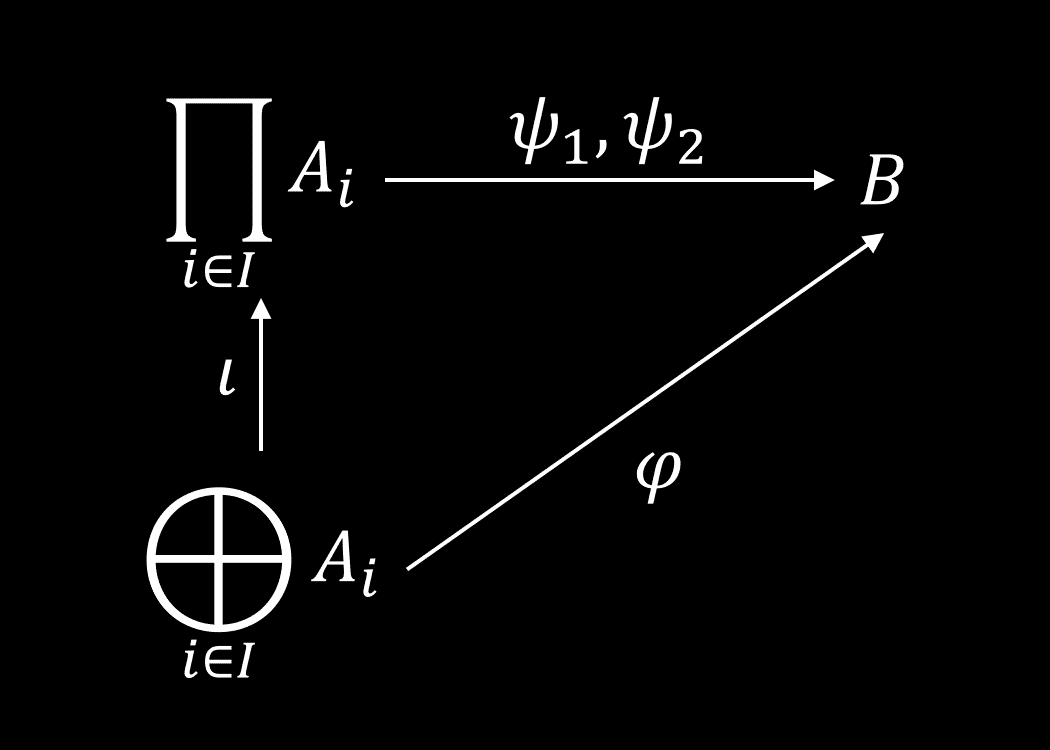Define $\nu:\prod_\idxi{A_i}\to B,a\mapsto\psi_1\left(a\right)-\psi_2\left(a\right),$ and we can find that $\displaystyle\bigoplus_\idxi{A_i}\leq\ker\nu$. Moreover, for all homomorphism $\displaystyle\mu:\prod_\idxi{A_i}\to B$ such that $\displaystyle\bigoplus_\idxi{A_i}\leq\ker\mu$, we have $\left(\psi_1+\mu\right)\iota=\varphi$.

Therefore, the ‘solutions’ of the above commutative diagram are exactly those can be written as $\psi^\star+\xi\pi$, where $\psi^\star$ is one specific solution, $\displaystyle\xi\in\Hom\left({\frac{\prod_\idxi{A_i}}{\bigoplus_\idxi{A_i}},B}\right)$, and $\displaystyle\pi:\prod_\idxi{A_i}\to\frac{\prod_\idxi{A_i}}{\bigoplus_\idxi{A_i}}$ is the canonical map.

This resembles the structure of solutions to (not necessaily homogeneous) linear equations very much.

Remarks and Acknowledgements

Extension of Homomorphism (Abelian) ⟺ Direct Summand

Let $A$ be an abelian group and $B\leq A$ a subgroup. TFAE:

1. For all group $G$ and homomorphism $\varphi:B\to G$, there exists a homomorphism $\varphi^\star:A\to G$ such that ${\left.\varphi^\star\right|}_B=\varphi$.
2. For all abelian group $C$ … (1 restricted to abelian groups)
3. There exists a homomorphism $\varphi^\star:A\to B$ such that ${\left.\varphi^\star\right|}_B=\id_B$.
4. There exists a subgroup $C\leq A$ such that $A=B\oplus C$.

1 ⟹ 2, 2 ⟹ 3 and 4 ⟹ 1 are trivial.

(3 ⟹ 4) Define $\psi:A\to A,a\mapsto a-\varphi^\star\left(a\right)$ and let $C=\im\psi$. For all $a\in A$, $a=\varphi^\star\left(a\right)+\psi\left(a\right)$, therefore $A=B+C$. For all $a\in B\cap C$, we have $a=\psi\left(b\right)$ for some $b\in A$, and $\IntersectIsZero$ Therefore, $A=B\oplus C$.

The technique to construct the complement subgroup resembles that to construct a complement vector subspace from idempotent linear transformations (projections) very much.

Acknowledgements

I would like to thank Professor Goodearl and Shan Zhou for their discussions on this problem with me.