Notes for UMich EECS 598 (2015): Homework 1

Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for homework 1.

Update on 5 January 2020. I managed to give an ugly solution to the extra credit problem.

Problem 1. Given a generating set B={b1​,…,bm​}, output the (positive) greatest common divisor of those elements. Euclidean algorithm for computing the GCD of two numbers runs in polynomial time, and the output is shorter than the input. Therefore, the total running time is polynomial.

Problem 2. Note that the two inequalities are equalities when n=1. For n=2, consider the basis $$\mathbf{B}=({\mathbf{b}}_1,{\mathbf{b}}_2)=\left(\begin{array}{cc}{2}^{6t}& 2^{2t}\\ 0& 1\end{array}\right),$$ where $t$ is a positive integer. The determinant bound is $2^{3t+1/2}$ and the shortest Gram–Schmidt vector has length 1. We now consider any non-zero lattice point x1​b1​+x2​b2​:

• When x1​=0, the smallest possible length is 24t+1​, attained when x2​=±1.
• When x1​​=0,∣x2​∣≤23t, its length is at least 26t−23t22t=25t.
• When ∣x2​∣>23t, its length is at least 23t.

The above covers all possible cases. Therefore, we have 22t≤λ1​(L)≤1+22t.

Problem 3(a). By definition, for any x∈Rn, there exists unique $\mathbf{v}\in \mathcal{L}$ s.t. x∈(v+F), which means $\mathbf{x}=\mathbf{v}+\mathbf{f}$ for some f∈F. This further translates into f=x−v∈(x+L). Therefore, $(\mathbf{x}+\mathcal{L})\cap \mathcal{F}$ is non-empty. Suppose f′∈(x+L)∩F, then ${\mathbf{f}}^{\prime }=\mathbf{x}-{\mathbf{v}}^{\prime }$ for some v′∈L. This means x∈(v′+F). By the uniqueness of v, it follows that v=v′, hence f=f′. This completes the proof that the intersection is a singleton set.

Problem 3(b). Given x, find (using Gaussian elimination) real coefficients $y_1,\dots ,y_n$ s.t. $$\mathbf{x}=\sum _{i=1}^n{y}_i{\mathbf{b}}_i.$$ We then have $$\begin{array}{rl}\mathbf{x}-\sum _{i=1}^n\lfloor y_i\rceil {\mathbf{b}}_i& =\sum _{i=1}^n(y_i-\lfloor y_i\rceil ){\mathbf{b}}_i\\ & \in \mathbf{B}\cdot {\left[\frac{-1}{2},\frac{1}{2}\right)}^n.\end{array}$$

Problem 3(c). We use QDU decomposition. Suppose $\mathbf{B}=\mathbf{Q}\mathbf{D}\mathbf{U}$ and B=QD, where $\mathbf{Q}$ is orthogonal, $\mathbf{D}$ is positive diagonal, and $\mathbf{U}$ is upper-unitriangular. Let F=B⋅[2−1​,21​)n.

First, we show $(\mathbf{x}+\mathcal{F})\cap ({\mathbf{x}}^{\prime }+\mathcal{F})\ne \varnothing$ only if $\mathbf{x}={\mathbf{x}}^{\prime }$ for x,x′∈L. Let $\mathbf{w}$ be a vector in this intersection, then $$\begin{array}{rl}\mathbf{w}& =\mathbf{B}{\mathbf{z}}^{}+\tilde{\mathbf{B}}{\mathbf{v}}^{}=\mathbf{Q}\mathbf{D}(\mathbf{U}\mathbf{z}+\mathbf{v})\\ & =\mathbf{B}{\mathbf{z}}^{\prime }+\tilde{\mathbf{B}}{\mathbf{v}}^{\prime }=\mathbf{Q}\mathbf{D}(\mathbf{U}{\mathbf{z}}^{\prime }+{\mathbf{v}}^{\prime })\end{array}$$ for some $\mathbf{z},{\mathbf{z}}^{\prime }\in {\mathbb{Z}}^n,\mathbf{v},{\mathbf{v}}^{\prime }\in {\left[\frac{-1}{2},\frac{1}{2}\right)}^n$ s.t. Bz=x,Bz′=x′. Moving terms around and cancelling QD, we get U(z−z′)=v′−v. Suppose for the sake of contradiction that z−z′​=0, and that its last non-zero entry were the $k$^th one. Using the upper-unitriangularity, we would get $$\begin{array}{rl}\mathbf{z}[k]-{\mathbf{z}}^{\prime }[k]& =(\mathbf{U}(\mathbf{z}-{\mathbf{z}}^{\prime }))[k]\\ & ={\mathbf{v}}^{\prime }[k]-\mathbf{v}[k]\in (-1,1).\end{array}$$ This is a contradiction because the left-hand side would be a non-zero integer. Therefore, x=Bz=Bz′=x′.

Next, we show that its translations using lattice points cover ${\mathbb{R}}^n$ algorithmically. This amounts to solving $\mathbf{z},\mathbf{v}$ from w=QD(Uz+v), where $\mathbf{w}$ is any vector in ${\mathbb{R}}^n$ and the other symbols inherit their meanings from the first part. We solve $\mathbf{U}\mathbf{z}+\mathbf{v}={\mathbf{D}}^{-1}{\mathbf{Q}}^{-1}\mathbf{w}$ from the last entry to the first. Suppose we have computed z[k+1],…,z[n],v[k+1],…,v[n], we then set $$\begin{array}{rl}t& =({\mathbf{D}}^{-1}{\mathbf{Q}}^{-1}\mathbf{w})[k]-\sum _{i=k+1}^n\mathbf{U}[k,i]\mathbf{z}[i],\\ \mathbf{z}[k]& =\lfloor t\rceil ,\mathbf{v}[k]=t-\lfloor t\rceil .\end{array}$$ This can be done efficiently and, by inspection, gives a correct solution.

Problem 4. The volume of an n-dimensional p-ball of radius $r$ is $$\frac{{\left(2r\cdot \Gamma \left(1+\frac{1}{p}\right)\right)}^n}{\Gamma \left(1+\frac{n}{p}\right)}.$$ (This formula is due to Xianfu Wang.) Setting this to be at least 2n, we get (using Stirling’s formula) $$\begin{array}{rl}{\lambda }_1^{(p)}(\mathcal{L})& (\Gamma \left(1+n/p\right)\det \mathcal{L}{)}^{1/n}\\ & ={\Theta }_p(n^{1/p}(\det \mathcal{L}{)}^{1/n}).\end{array}$$

Problem 5. We first show that its translations by lattice points do not overlap. Suppose for the sake of contradiction that $\mathbf{z}\in ({\mathbf{y}}_1+\mathcal{V}(\mathcal{L}))\cap ({\mathbf{y}}_2+\mathcal{V}(\mathcal{L}))$ for ${\mathbf{y}}_1,{\mathbf{y}}_2\in \mathcal{L}$ but y1​​=y2​. We would have $$|{\mathbf{x}}_1|=|\mathbf{z}-{\mathbf{y}}_1|=|{\mathbf{x}}_2+({\mathbf{y}}_2-{\mathbf{y}}_1)|<|{\mathbf{x}}_2|,$$ but $|{\mathbf{x}}_2|<|{\mathbf{x}}_1|$ by swapping the roles of ${\mathbf{x}}_1,{\mathbf{x}}_2$ in the above argument. Therefore, the translations of $\mathcal{V}(\mathcal{L})$ by lattice points do not overlap.

Next, for all points whose closest lattice point is unique, it is easy to verify that it lies in the translate of $\mathcal{V}(\mathcal{L})$ by the closest lattice point to it. If a point is closest to two distinct lattice points, it cannot be in a translate of $\mathcal{V}(\mathcal{L})$ by any lattice point.

(Assume the lattice is full-rank by convention.) The points whose closest lattice points are not unique form a null set (set of measure 0, i.e., rare). To see this, consider enumerating non-singleton closest lattice point set S. The set of points that have the same lengths to all points in $S$ has measure zero, so the union of countably many of them still has measure zero.

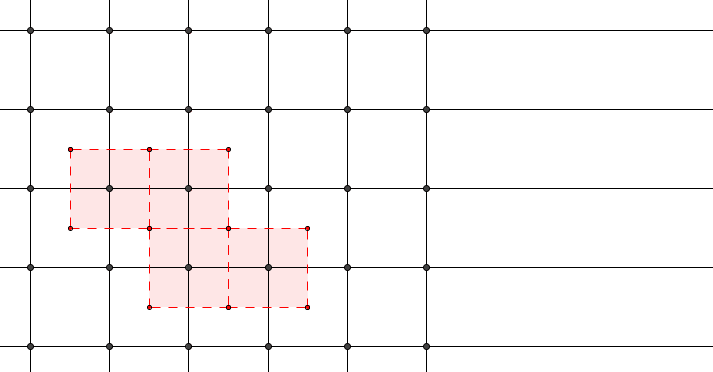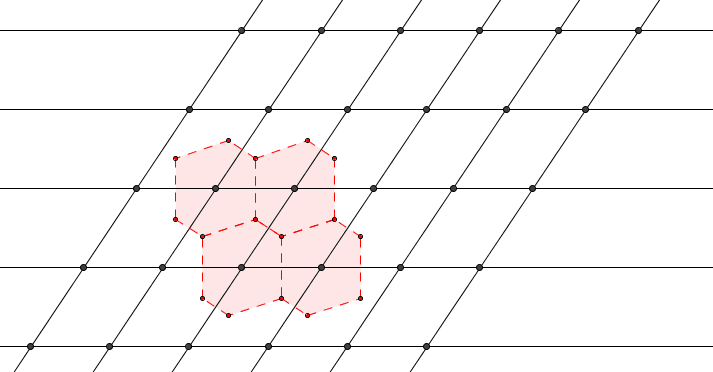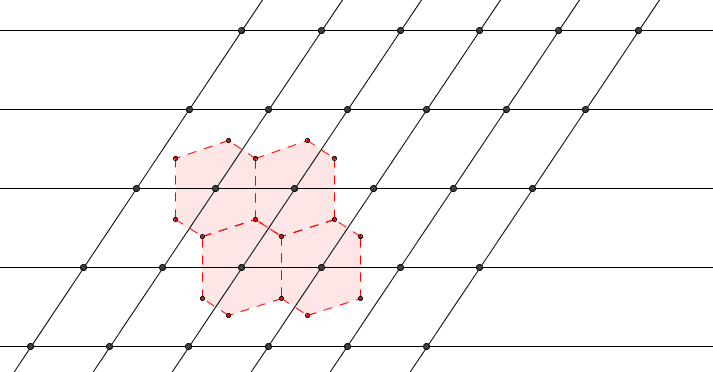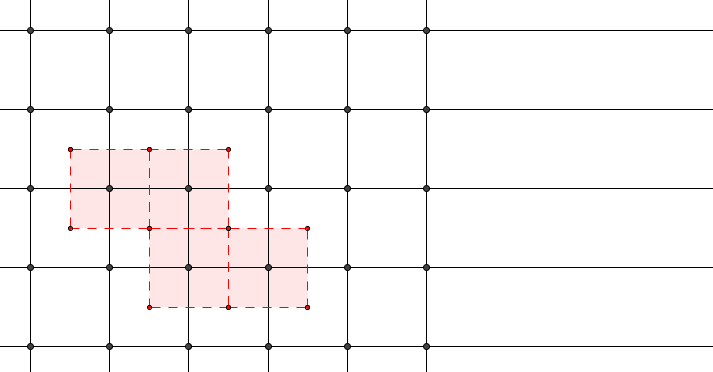
Extra Credit. I currently have no idea how to intrinsically extend Voronoi cell into a fundamental region. One can pathologically extend Voronoi cell to a fundamental region, using the axiom of choice. I still do not know how to do this non-pathologically.

Let $S$ be the family of supersets of $\mathcal{V}$ s.t. its translations by lattice points do not overlap (i.e., a subset of a candidate fundamental region). Assign set-theoretic order to this family of sets.

For any chain C⊆S, take T=⋃c∈C​c. We now verify that T∈S. It is obvious that V⊆T. Moreover, if $\mathbf{x}\in (T+\mathbf{u})\cap (T+\mathbf{v})$ for lattice points u,v, we have $\mathbf{x}={\mathbf{t}}_1+\mathbf{u}={\mathbf{t}}_2+\mathbf{v}$ for t1​,t2​∈T. Suppose ${\mathbf{t}}_1\in c_1,{\mathbf{t}}_2\in c_2$ for c1​,c2​∈C. Since $C$ is a chain, WLoG we assume c1​⊆c2​, then x∈(c2​+u)∩(c2​+v)​=∅, which implies $\mathbf{u}=\mathbf{v}$ by the definition of $S$ and the fact that c2​∈C⊆S. Therefore, we have T∈S. It clearly is an upper bound of C.

By Zorn’s lemma, there exists a maximal element F∈S. We now verify that $\mathcal{F}$ is a fundamental region. Since F∈S, its translations by lattice points do not overlap. Let x∈Rn. If x∈F, then x∈(F+0). Otherwise, we have ${\mathcal{F}}^{\prime }\stackrel{\text{def}}{==}\mathcal{F}\cup \{\mathbf{x}\}\notin S$ due to the maximality of F. Clearly V⊆F′, so there exists distinct lattice points $\mathbf{u},\mathbf{v}$ s.t. ∅​=(F′+u)∩(F′+v)∋z. Note that (F+u)∩(F+v)=∅=({x}+u)∩({x}+v), therefore, WLoG we assume $\mathbf{z}=\mathbf{x}+\mathbf{u}=\mathbf{f}+\mathbf{v}$ for some f∈F, giving us x=f+(v−u)∈(F+(v−u)). This completes the proof.

Note that the region can be made ‘prettier’ by restricting $S$ to contain only subsets of V. This way, the found fundamental region is bounded and measurable.