Notes for UMich EECS 598 (2015): Lecture 1

Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for lecture 1, mathematical background.

In this note, I write down proofs missing from his lecture note as well as my questions. Due to the nature of personal notes, I will not formally put references.

Definition 2.1. An n-dimensional lattice $\mathcal{L}$ is a discrete additive subgroup of Rn.

Proposition. Let $\mathcal{L}$ be a subgroup of Rn, then TFAE:

1. For all x∈L, there exists $\epsilon >0$ s.t. L∩B(x,ε)={x}.
2. There exists $\epsilon >0$ s.t. L∩B(0,ε)={0}.
3. There exists $\epsilon >0$ s.t. for all x∈L, it holds that L∩B(x,ε)={x}.

Proof. We prove this by cycling around.

• 3 ⟹ 1 ⟹ 2. Trivial.
• 2 ⟹ 3. Take the $\epsilon$ guaranteed by (2) as that for (3). For all $\mathbf{x},\mathbf{v}\in \mathcal{L}$ s.t. v∈B(x,ε), we have $\mathbf{v}-\mathbf{x}\in \mathcal{L}$ since $\mathcal{L}$ is a subgroup and v−x∈B(0,ε). By the choice of $\epsilon$ and (2), it follows that v−x=0.

Definition 2.3. The rank of lattice $\mathcal{L}$ is r=dimspanL.

Proposition. If L⊆Qn, there exists $d\in {\mathbb{N}}^{\ast }$ s.t. d⋅L⊆Zn.

Proof. This will be trivial once we show that a lattice always has a basis.

Definition 2.4. A basis $\mathbf{B}=\{{\mathbf{b}}_1,\dots ,{\mathbf{b}}_r\}$ of lattice $\mathcal{L}$ is a linearly independent subset of it such that it generates $\mathcal{L}$ (as an abelian group).

Proposition. Any (finite-dimensional) lattice has a basis.

Proof. Clearly $\mathcal{L}$ is torsion-free, so by the fundamental theorem of finitely generated abelian groups, we only need to show that $\mathcal{L}$ is finitely generated. Since L⊆Rn, it has a maximal linearly independent subset S={s1​,…,sr​}. For all x∈L, there exists real coefficients $y_1,\dots ,y_r$ s.t. $$\mathbf{x}=\sum _{i=1}^r{y}_i{\mathbf{s}}_i.$$ Let v==defx−∑i=1r​⌊yi​⌋si​, then $\mathbf{v}\in \mathcal{L}$ and $$|\mathbf{v}|\le \sum _{i=1}^r|{\mathbf{s}}_i|\stackrel{\text{def}}{==}R.$$ This means the set $S\cup (\mathcal{L}\cap B(0,R))$ generates L. We’re done because this is a finite set — in particular, it contains at most $r+R^n/{\epsilon }^n$ points, where $\epsilon$ is the positive number guaranteed by (3) of a previous proposition.

Corollary 2.7. (Checking equivalence of lattices generated by two bases, generalized to rank-deficient case.) To check whether ${\mathbf{B}}_1,{\mathbf{B}}_2\in {\mathbb{R}}^{n\times r}$ generate the same lattice:

1. Check whether r=rank(B1​,B2​). This ensures colspanB1​=colspanB2​.
2. Find an isometry (isomorphism between Euclidean spaces) $\rho :\mathrm{colspan}{\mathbf{B}}_1\to {\mathbb{R}}^r$ and compute C1​=ρ(B1​),C2​=ρ(B2​),C1​,C2​∈Rr×r. Note that the $\rho$ can be found using Gram–Schmidt orthonormalisation (QR decomposition).
3. Check whether ${\mathbf{C}}_1^{-1}{\mathbf{C}}_2$ is unimodular.

Definition 2.8. (Fundamental region, generalized to rank-deficient case.) A fundamental region $\mathcal{F}\subseteq {\mathbb{R}}^n$ of lattice $\mathcal{L}$ is one such that it has exactly one representative for each coset in (spanL)/L.

Definition 2.9. The fundamental parallelepiped of a lattice basis $\mathbf{B}\in {\mathbb{R}}^{n\times r}$ is B⋅[2−1​,21​)r. Sometimes, one might opt for an alternative definition B⋅[0,1)r.

Example. Voronoi cell of $\mathcal{L}$ is the set $$\mathcal{V}(\mathcal{L})\stackrel{\text{def}}{==}\{\mathbf{x}\in \mathrm{span}\mathcal{L}:\forall \mathbf{v}\in \mathcal{L}\setminus \{0\},|\mathbf{x}|<|\mathbf{x}-\mathbf{v}|\}.$$ It is not a fundamental region, but its closure is the closure of a fundamental region.

Definition 2.11. The volume (determinant) of lattice $\mathcal{L}$ is the volume of any of its fundamental region.

Claim 2.12. (Determinant from basis, generalized to rank-deficient case.) If $\mathcal{L}$ has basis B, it has determinant det(BT​B)​.

Question. There need to be some extra conditions posed on the fundamental region to make the volume well-defined. Consider the lattice Z, which has a fundamental region $$V\cup (1+[0,1)\setminus V).$$ Here, $V$ is a Vitali set containing 0. This fundamental region is not measurable, so it makes no sense to talk about its volume. Another interesting question: is there a Banach–Tarski paradox for lattice fundamental regions?

The simplest way to fix this is to consider a region that contains at most one representative of each coset and whose closure contains at least one representative of each coset. This ensures the volume is well-defined (though I don’t know how to prove this).

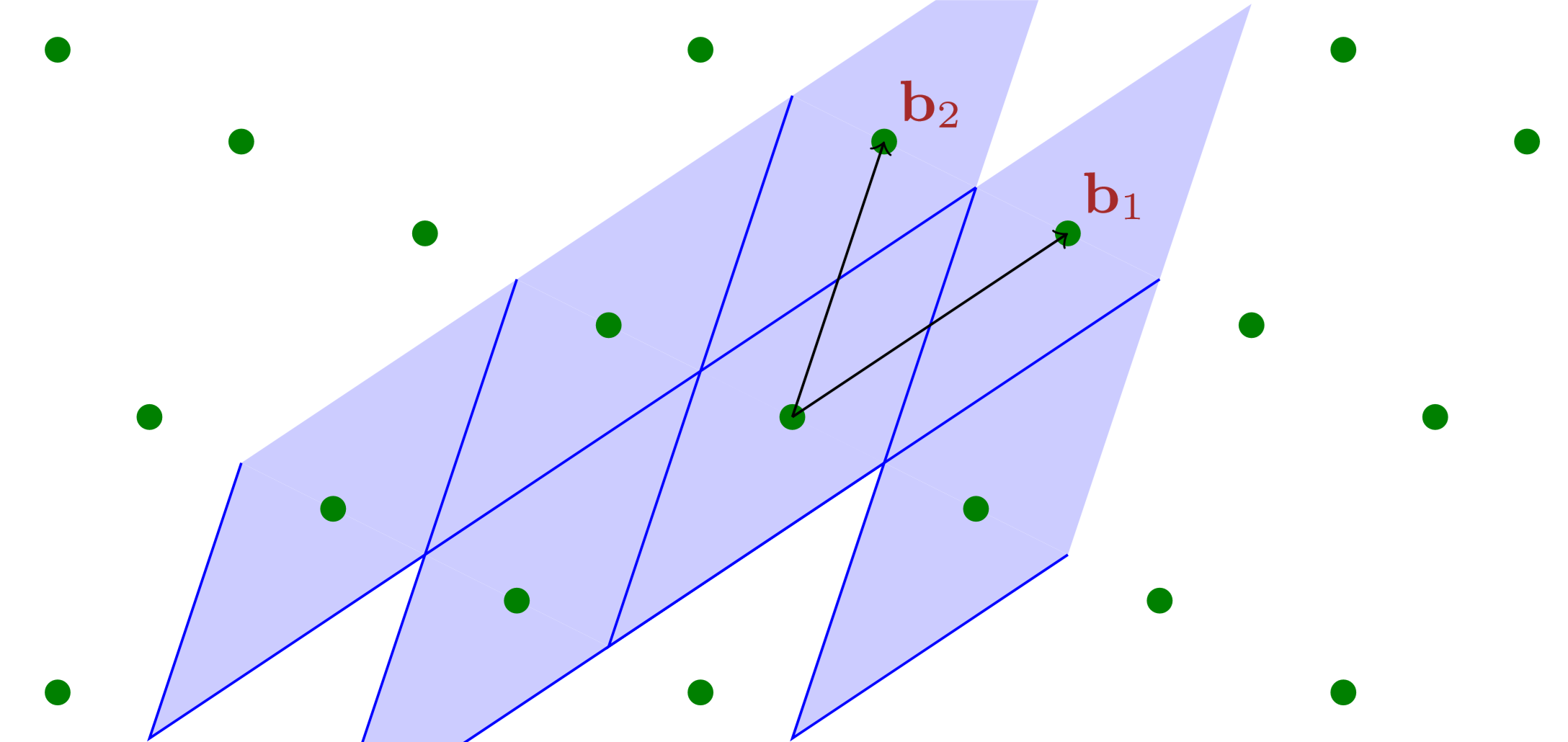
Definition 2.13. The minimum distance of lattice $\mathcal{L}$ is λ1​(L)==definfx∈L∖{0}​∣x∣.

I haven’t carefully investigated Minkowski’s results — I will update if I find a question or comment.