属性加密（番外）：分段安全性的故事
这一篇是我的 2019 年科研“属性加密”系列番外篇，记录一些关于（特殊）分段安全性的故事。这一篇的风格相较主系列更轻松活泼（肯定有人要吐槽我对“轻松活泼”的定义），比如去掉了繁复的导航按钮，减少了公式。另外这一篇也加上了“数学”的标签，大概是因为很多这里考虑的问题的密码学价值不大，更像是线性代数的游戏？
Blog entries with tag ‘Cryptography’
- 密码学
属性加密：分段安全性
千呼万唤始出来！本文是我的 2019 年科研“属性加密”系列博文第五篇。之前一套“增加编程空间、递归模拟、树平衡化”组合拳，针对算术公式证明了 1-ABE 的适应性安全性，在这之后，我跌跌撞撞发现了最终记录在 [LL20] 里的一个关键性质：AKGS 分段安全性。这个性质大大简化了证明过程。
属性加密：修复诈和
本文是我的 2019 年科研“属性加密”系列博文第四篇。这次揭晓上回的小悬念：解释上次的证明怎么错了，然后讨论针对算术公式的一个自然的修复思路。这个思路最终启发我发掘出了 [LL20] 中的一个关键概念，但这段故事本身并未记载在文献中，因此这一篇也肩负着重要使命：讲述文献“冰冷的美丽”背后“火热的思考”。
属性加密：1-ABE
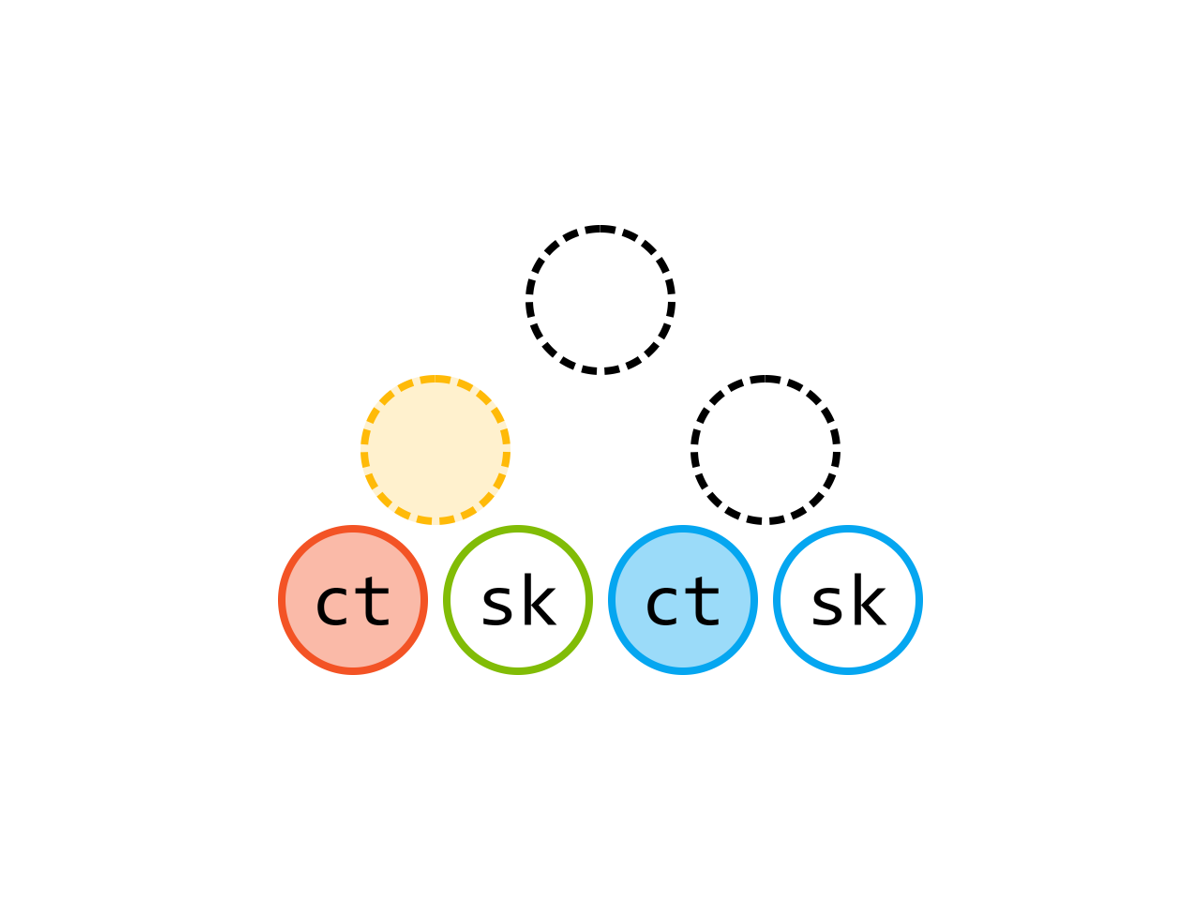
本文是我的 2019 年科研“属性加密”系列博文第三篇。在这一篇里，我将介绍 [LL20] 里构造一次性安全的属性加密方案（叫做 1-ABE）的思路——使用内积加密计算算术密钥乱码化方案的标签。本文有彩蛋！
属性加密：算术密钥乱码化
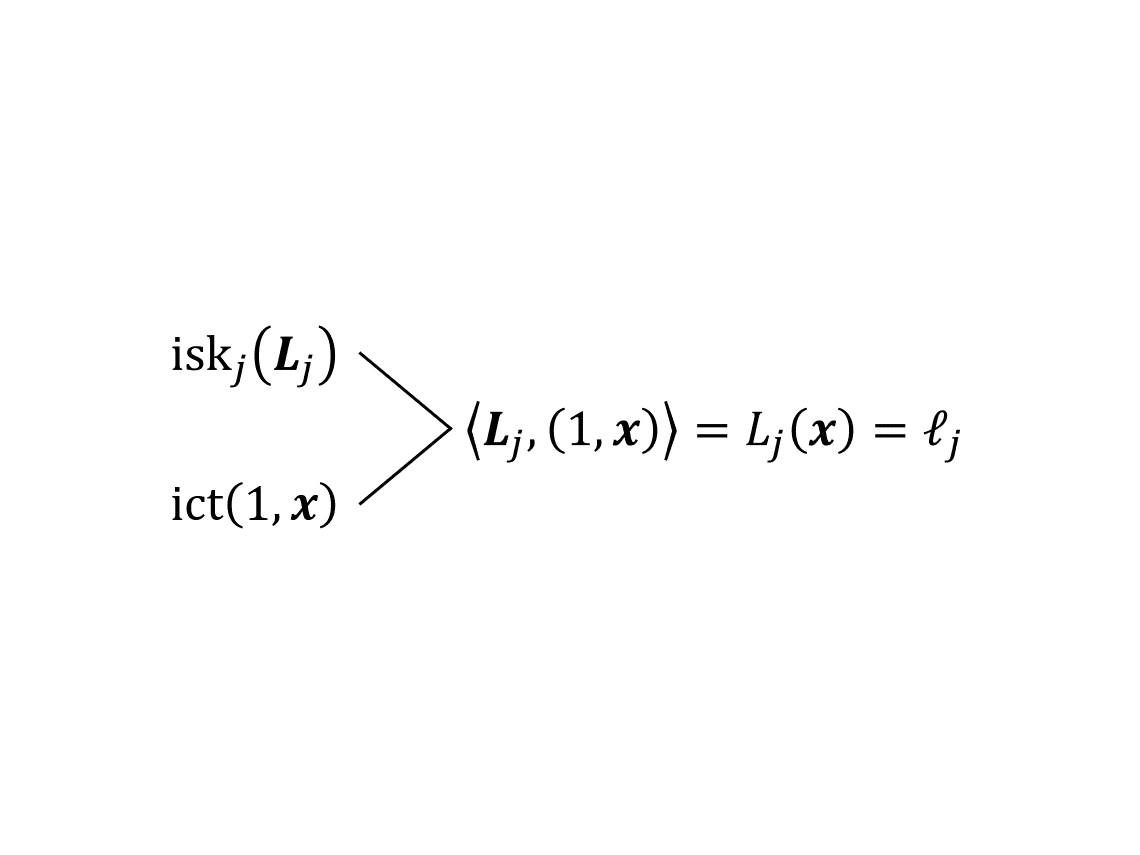
本文是我的 2019 年科研“属性加密”系列博文第二篇。在这一篇里，我将引入 [LL20] 中建立信息论意义下安全性的核心工具——算术密钥乱码化方案 (AKGS)——并给出适用于算术公式的构造。
属性加密：引子
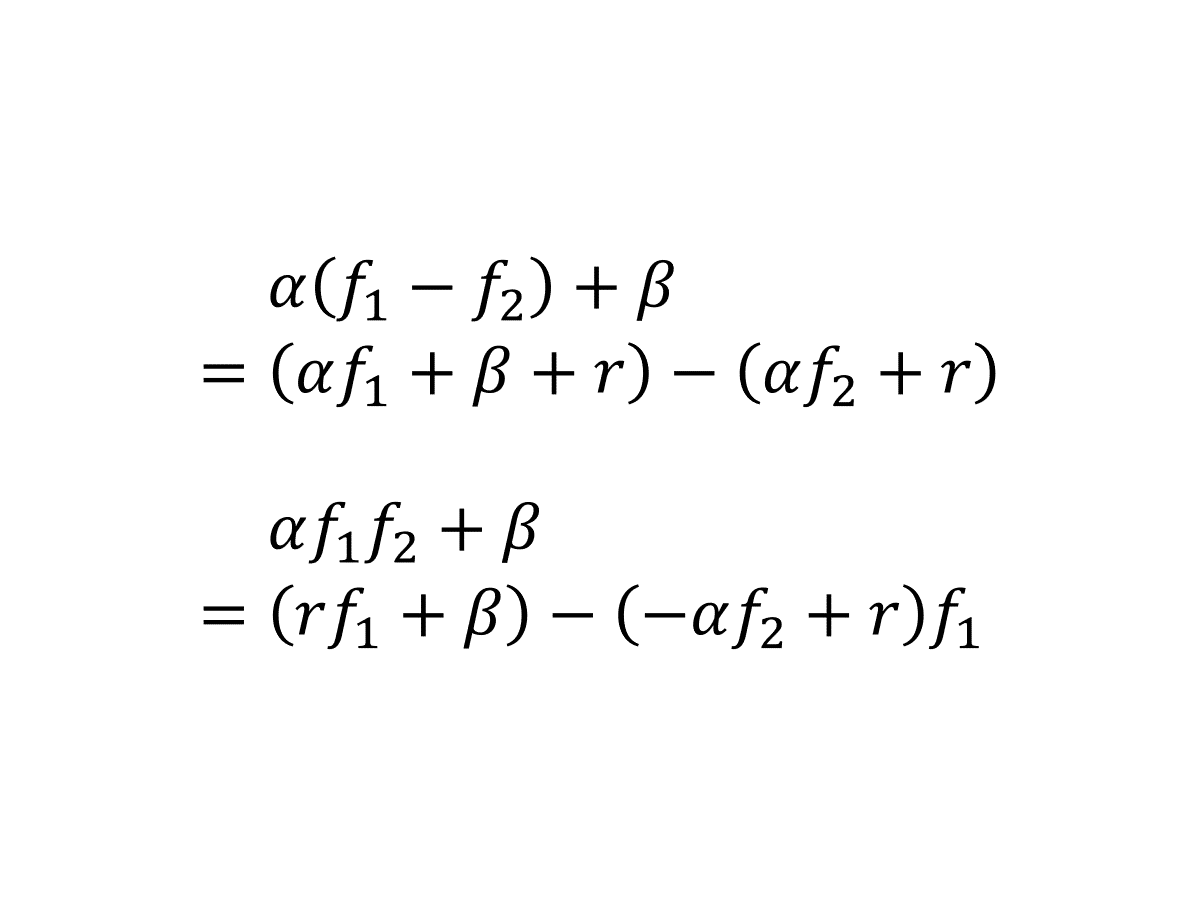
本文是我的 2019 年科研“属性加密”系列博文的首篇，该系列博文旨在用汉语介绍我和我导师的合作论文 Compact Adaptively Secure ABE from 𝑘-Lin: Beyond NC¹ and Towards NL [LL20]。在这一篇里，我将介绍属性加密的基本概念并定下一个“小目标”。
内积加密：双槽内积加密
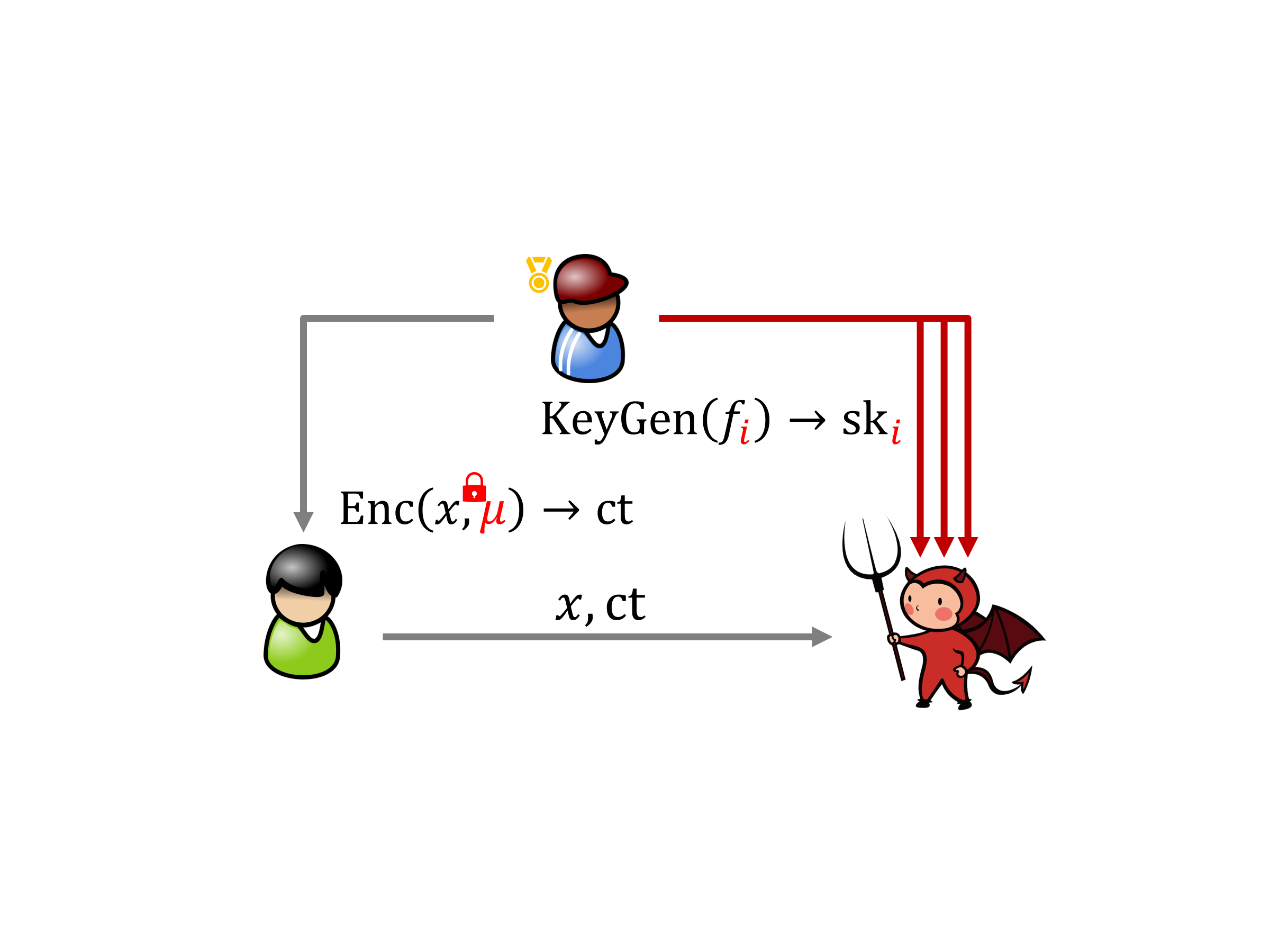
欢迎来到“内积加密”系列文章的后半部分，这部分科普 Lin 与 Vaikuntanathan 在 2016 年提出的内积加密算法。终于是最后一篇了，我们说说双槽内积加密。
内积加密：双层加密、三仙归洞与空当接龙
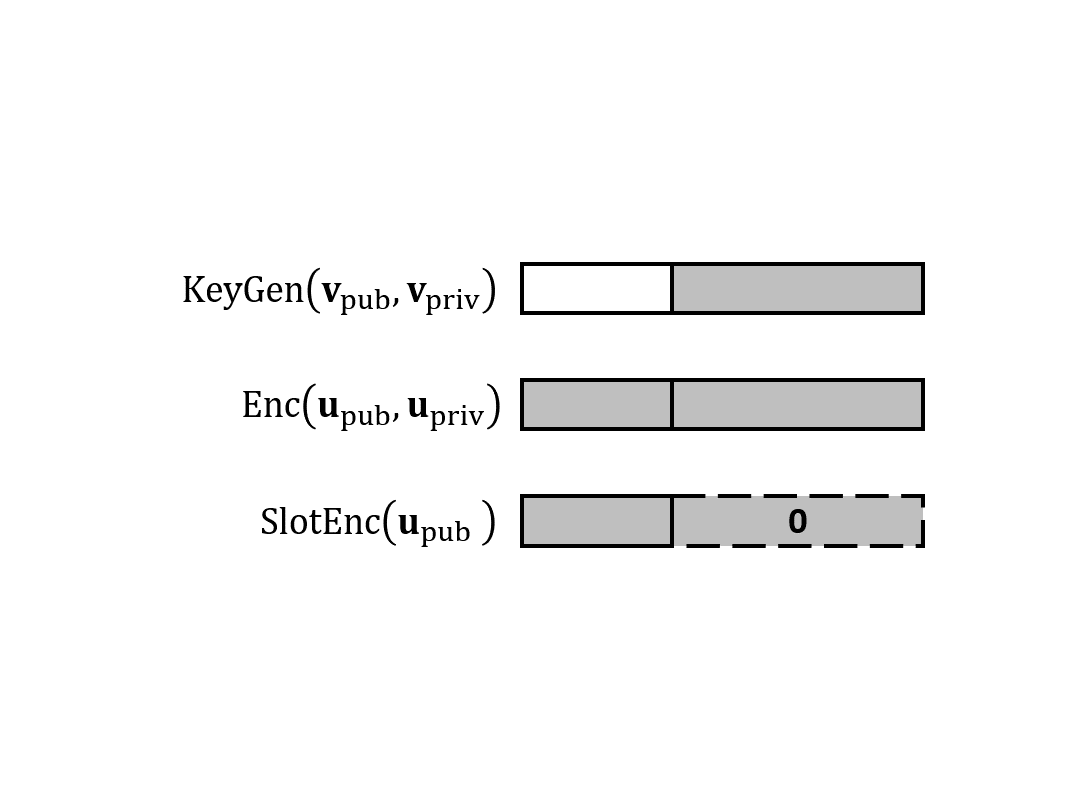
欢迎来到“内积加密”系列文章的后半部分，这部分科普 Lin 与 Vaikuntanathan 在 2016 年提出的内积加密算法。在第二篇里，我们说说如何构造具有泛函保密性的私钥 IPFE 以及它的安全性证明。（本来计划的双槽内积加密推到第三篇了。）
内积加密：泛函保密、配对
欢迎来到“内积加密”系列文章的后半部分，这部分科普 Lin 与 Vaikuntanathan 在 2016 年提出的内积加密算法。这一篇我们开始讨论前半部分未解的一个疑问：如何保护密钥里的向量？延续之前的习惯，我们先定义泛函保密性。为了构造这样的方案，我们要引入另一个工具——配对（即双线性映射）。
内积加密：ALS 公钥方案
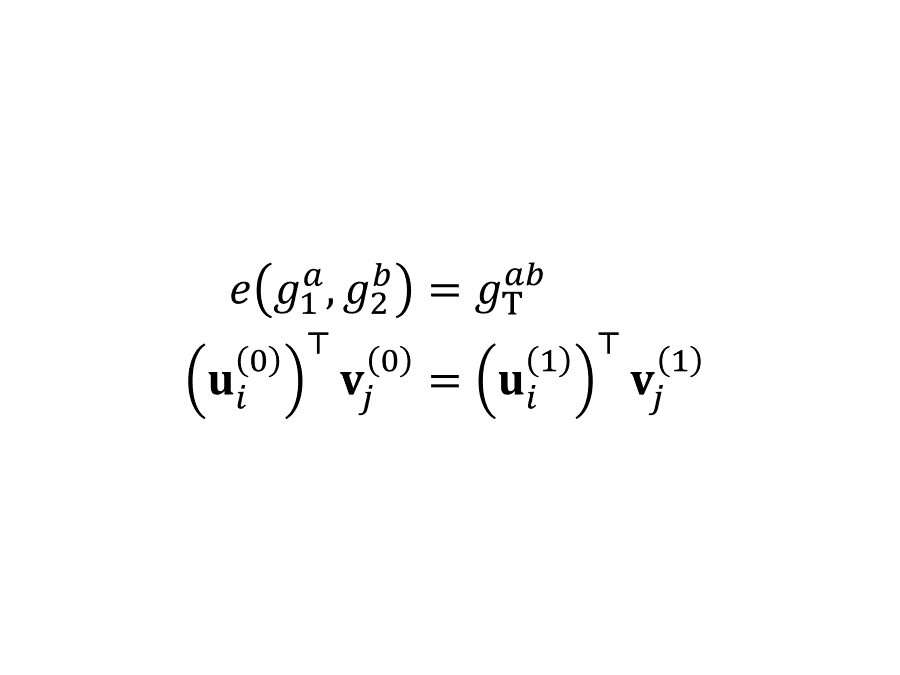
“内积加密”系列文章的前半部分旨在总结和科普 Agrawal、Libert、Stehlé 在 2016 年提出，Wee 在 2017 年改进，Agrawal、Libert、Monosij、Titiu 在 2020 年完善的内积加密算法。本篇是前半部分的最后一篇，叙述 ALS 公钥内积加密方案并证明它的 SIM-CPA 安全性。它的构造思想既可以理解为光滑投影哈希（也叫“哈希证明系统”）加换元法，也可以理解为双系统加密。
内积加密：MDDH 假设
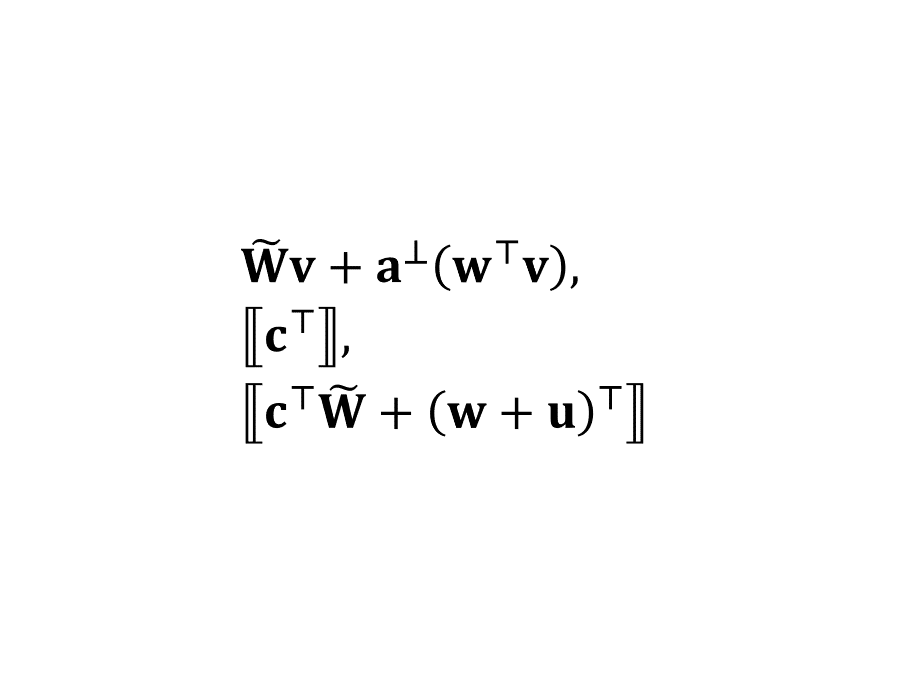
“内积加密”系列文章的前半部分旨在总结和科普 Agrawal、Libert、Stehlé 在 2016 年提出，Wee 在 2017 年改进，Agrawal、Libert、Monosij、Titiu 在 2020 年完善的内积加密算法。在这一篇里我们讨论一些针对 ALS 方案的准备知识：循环群、MDDH 假设。
内积加密：公钥 IPFE 与 CPA 安全性
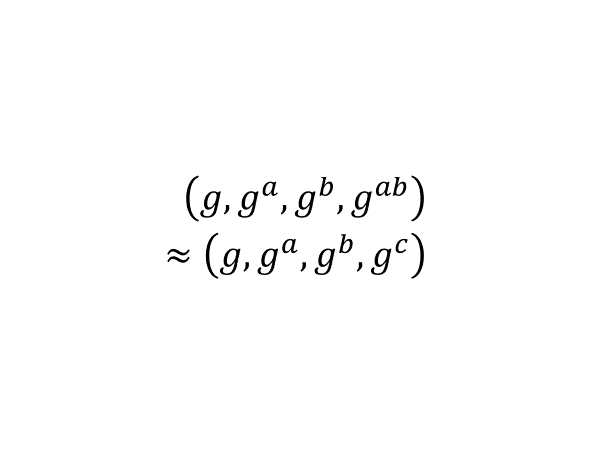
“内积加密”系列文章的前半部分旨在总结和科普 Agrawal、Libert、Stehlé 在 2016 年提出，Wee 在 2017 年改进，Agrawal、Libert、Monosij、Titiu 在 2020 年完善的内积加密算法。在这一篇里我们讨论公钥 IPFE 的语法、语义、安全性，为此我们需要引入计算意义下的不可区分性，并练习多项式时间归约和过渡证明法。
内积加密：一次一密
“内积加密”系列文章的前半部分旨在总结和科普 Agrawal、Libert、Stehlé 在 2016 年提出，Wee 在 2017 年改进，Agrawal、Libert、Monosij、Titiu 在 2020 年完善的内积加密算法。在这一篇里我们讨论如何用一次一密构造完美一次性模拟安全的（私钥）内积加密。
内积加密（线性泛函加密）：引子
本篇博文是一系列关于内积加密的科普文章的首篇。该系列文章的前半部分旨在总结和科普 Agrawal、Libert、Stehlé 在 2016 年提出，Wee 在 2017 年改进，Agrawal、Libert、Monosij、Titiu 在 2020 年完善的内积加密算法。在这一篇里我们讨论内积加密、完美保密性和完美模拟安全性的定义，并初步讨论这两种安全性之间的关系。
Notes for UMich EECS 598 (2015): Clean-up
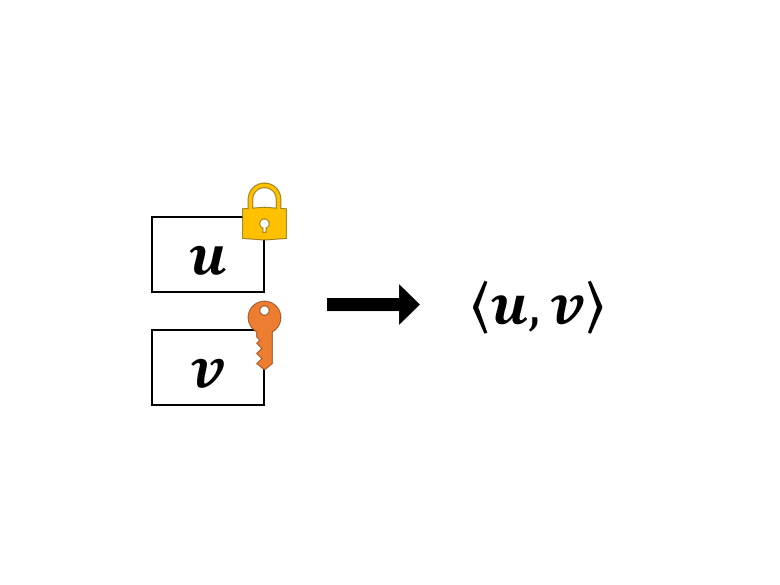
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for homework 3, homework 4 and lecture note 5.
Notes for UMich EECS 598 (2015): Homework 2
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for homework 2.
Notes for UMich EECS 598 (2015): Lecture 4
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for lecture 4, Coppersmith, cryptanalysis.
Notes for UMich EECS 598 (2015): Homework 1
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for homework 1.
Notes for UMich EECS 598 (2015): Lecture 3
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for lecture 3, LLL, Coppersmith.
Notes for UMich EECS 598 (2015): Lecture 2
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for lecture 2, SVP, Gram–Schmidt, LLL.
Notes for UMich EECS 598 (2015): Lecture 1
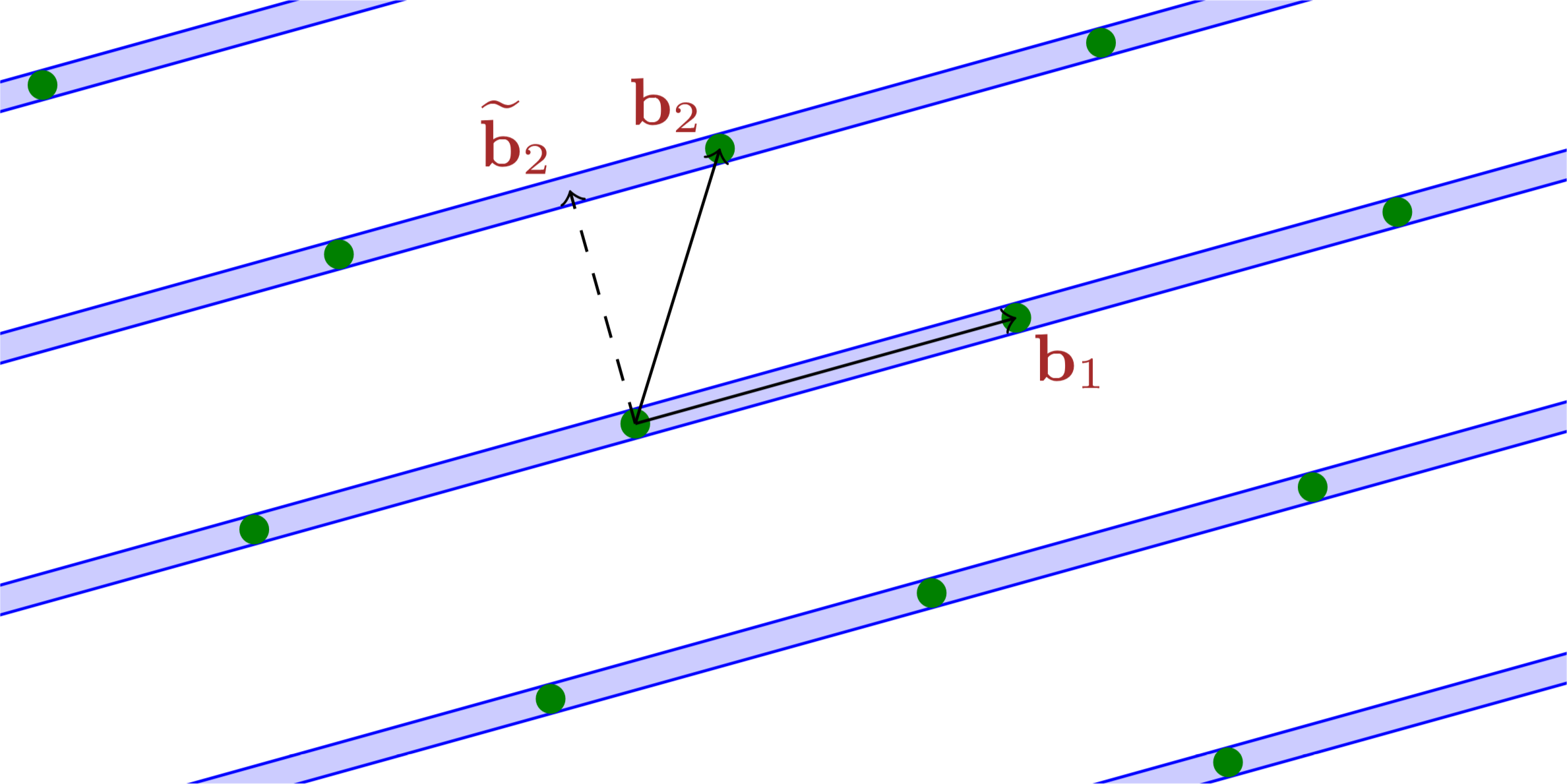
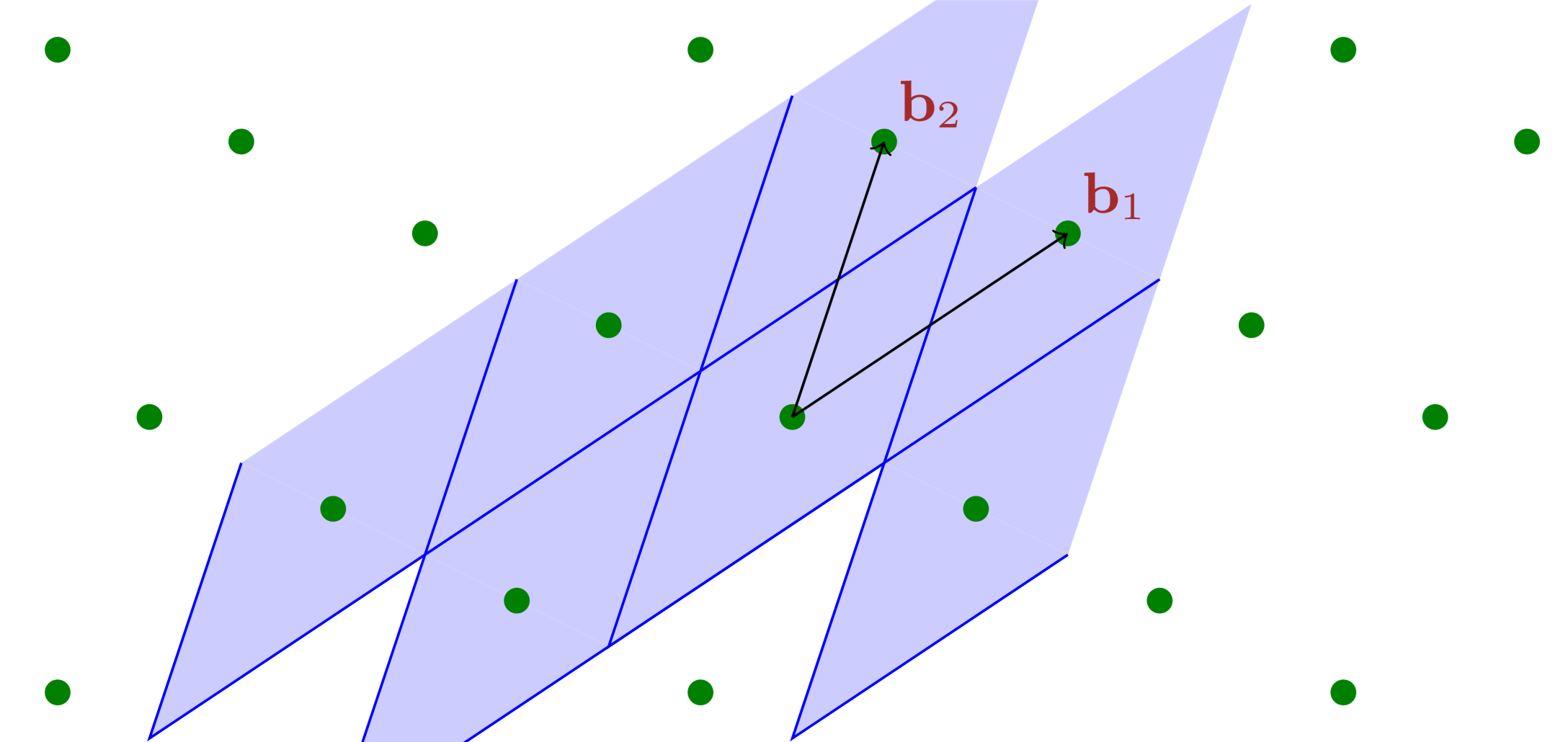
Notes for UMich EECS 598 (2015) are for Lattices in Cryptography virtually instructed by Chris Peikert (i.e., I taught myself using resources made available by him). This entry is for lecture 1, mathematical background.
Two (equivalent) definitions of computational indistinguishability, two (isomorphic) ways of doing hybrids
It wasn’t until recently did I realise there are two isomorphic ways (different styles) of writing hybrid proofs. They actually correspond to the two equivalent definitions of computational indistinguishability — one based on guessing and the other based on distinguishing. Actually, I’ve been writing both kinds of proofs subconciously.
A note on (non-)uniform reductions
I learnt how to write uniform hybrid reductions in my rudimentary cryptography course, which are beasty beauties that wrap an adversary, trying break each of the many underlying cryptographic assumptions simultaneously. However, those constructions are less easy to write and read than using the transitivity of computational indistinguishability up to polynomially many times. The latter involves writing out the (perhaps polynomially many) hybrids and arguing that adjacent hybrids are indistinguishable. I also learnt non-uniform reductions, noticeably the technique to only work with deterministic adversaries. I’m writing a proof using hybrid argument lately, and I asked my advisor about whether I should write the beast or just the hybrids…
The two asymptotically equivalent definitions of IND-CPA
There are two asymptotically equivalent definitions of IND-CPA for secret-key encryption schemes. I think the one-challenge one makes the proof neater.
[KW19] 标准假设下适用于 NC¹ 策略的紧凑、适应性安全的属性加密
Kowalczyk 和 Wee 在 EUROCRYPT 2019（欧密会）上发表的文章 Compact Adaptively Secure ABE for NC¹ from 𝑘-Lin 可以说是彻底解决了 NC¹ 访问策略的属性加密问题。我在最近的密码学读书会上将讲述该文，这篇博文算是我用母语对该文章的总结（感觉我脑内思考语言仍然是汉语），也算是在中文密码学社区里传播知识。
![[KW19] 标准假设下适用于 NC¹ 策略的紧凑、适应性安全的属性加密](/entries/kw19-abe-nc1/assets/hero.png)
The Code Book (Simon Singh) 读书笔记
操作系统课中讲安全的一节是代课老师上的，期间他推荐了 The Code Book (Simon Singh) 这本书，说是讲密码学历史的。我对密码学感兴趣，就读了一读，并照“不动笔墨不读书”的原则，记了读书笔记，发表出来以飨观众。
我的第一篇（密码学）学术论文
在 Aarhus 的密码学研究从春天到秋天一直断断续续在进行。今日传来喜讯：我们的文章已被 PKC 2018 接收。
Of Kerckhoffs’ principle
Let me explain the classic idea that ‘the algorithm of a crypto system should be considered and made public’ to you. Particularly, I will discuss what it means by ‘crypto system’, which tells us what information should be no secret at all.